Paradox – die neusten Beiträge

Ich finde das Thema interessant, die gängigen Beispiel aber zu "relativ"

Ich reduziere Beispiele ( soweit möglich ) auf den Kern der Aussagen und lege Bezugspunkte fest.

Ûber die kann man diskutieren, wenn am Ende gemeinsame Bezugspunkte festgelegt werden.

Ein bezugpunkt ist die 'Zeit'

Zeit ist bei wikipedia definiert als "physikalische Größe zur Beschreibung der Abfolge von Ereignissen "

Eine physikalische Größe ist Definiert als :

"quantitativ bestimmbare Eigenschaft eines physikalischen Objektes, Vorgangs oder Zustands"

Ein physikalisches Objekt ist Definiert als Körper der Masse hat und Raum ein nimmt. ...

.....Quantifizierung bedeutet Angabe als Zahlenwert und kommt von lateinischquantum („wie viel“, „wie groß“). Dabei werden die Eigenschaften und Beschaffenheit eines Gegenstands oder Sachverhalts in messbare Größen und Zahlenwerte umformuliert.

Da Zeit kein Gegenstand ( objekt) oder Zustand ist , ist sie ein :

"Sachverhalt ( Vorgang ) zur Beschreibung der Abfolge von Ereignissen "

Ich sehe also einen Zustand. Dieser ändert sich und ändert sich nochmal.

Ich beobachte nun einen ' Abstand' zwischen den Änderungen, beschreibe nun diesen Sachverhalt der Abfolge von Ereignissen und nenne es Zeit.

Jetzt quantiviziere ich die Zeit und sage : " zwischen Urzustand und der ersten Änderung sind 10 Sekunden vergangen. Von der ersten bis zur zweiten Änderung sind 12 sekunden vergangen.

"Vor" dem Urknall gab es keine Abfolge von Ereignissen, und somit keine Zeit.

Nehmen wir nun an, das beim Urknall 3 ruhende Kugeln ( A,B,C) aus je 1 Milliarde Atome entstehen.

Ich beobachte nun, das sie , regelmäsig ,gleichzeitig je 1 Atom verlieren.

Den Abstand beschreibe ich als : alle 10 Sekunden .

Nun wird B und C die gleiche Menge Energie zu gefűhrt (gleich beschleunigt )

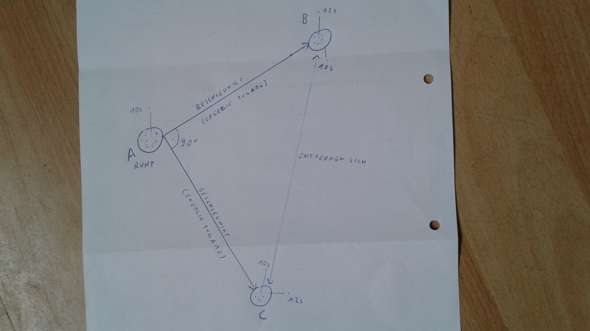
Kugel A ruht , Kugel B und C fliegen mit gleicher Geschwindigkeit im Winkel von 90 grad von A weg.

Laut Relativitätstheorie muss nun der Verlust, der Atome , betrachtet zwischen B und C weiterhin im Abstand von 10 Sekunden erfolgen. Da sie ja relativ zueinander ruhen, obwohl ich beobachten kann, das sie sich voneinander entfernen. ( Von B Richtung C oder von C Richtung B betrachtet)

Sie driften ja nur auf Grund des Winkels auseinander und wurden nicht nicht voneinander wegbeschleunigt , sondern von A .

Zu Kugel A hingegen soll sich nun ,die Beobachtung, der Abfolge der Ereignisse (zeit) verkűrzen.

Ich ( ruhend) beobachte nun das A weiterhin alle 10 Sekunden ein Atom verliert, B und C aber später (langsamer) zb. Nach 12 sekunden.

Wie kann das sein, da sie ja zueinander immer noch alle 10 Sekunden einen Verlust beobachten?

Ich habe ja noch den Weg, den sie zurűckgelegt haben, als kontroll Wert.

Sie műssen also immer nach dem gleichen Wegabschnitt ein Atom verlieren.

Was passiert denn ,bei der Zugabe von Energie, an den Kugeln (Atomen),das sie nun erst nach 12 Sekunden ein Atom verlieren ( zu A betrachtet ) ??

Hallo, wegen des neuen Updates funktionieren viele Spielstände und Mods nicht mehr. Deshalb würde ich gerne wissen wie man die Version zurücksetzen kann.

Ich spiele über Steam.

Falls das auf dich zutrifft... glauben deine Kinder an den Weihnachtsmann?

Falls ja: Wieso lässt du das zu?

Neuroleptika werden in der Schizophrenie-Therapie eingesetzt, da sie antipsychotisch und sedierendwirken. Sie lassen sich in Generationen aufteilen und können innerhalb dieser nochmal nach ihrer jeweiligen neuroleptischen Potenz gegliedert werden:

1. Generation:

• hochpotente Neuroleptika (z.B. Haloperidol, Fluphenazin, Perphenazin)
• mittelpotente Neuroleptika (z.B. Perazin, Melperon, Zuclopenthixol)
• niederpotente Neuroleptika (z.B. Promethazin, Levomepromazin)

2. Generation: atypische Neuroleptika (z.B. Olanzapin, Clozapin, Quetiapin, Risperidon)

Da Psychosen vor allem auf die Wirkung der Neurotransmitter Dopamin und Serotonin zurück zu führen sind, müssen auch entsprechend deren Rezeptoren im ZNS gehemmt werden. Verschiedene Arzneistoffe binden somit kompetitiv D2- (Dopamin-) oder 5HT2- (Serotonin-) Rezeptoren und regulieren somit als Antagonisten den Einfluss der Neurotransmitter auf die Psyche.

Fluspirilen ist ein solcher Dopaminantagonist, der die Dopamin-Rezeptoren blockiert und dadurch einen sedierenden, antriebsmindernden und vor allem antipsychotischen Effekt erzielt. Nach Benperidol und Haloperidol ist Fluspirilen ein weiterer Arzneistoff, der starke Dyskinesien verursacht.

Folgende Situation: Mutter (a) und Vater (b) zeugen zusammen einen Sohn (c). Auf einer wilden Familienfeier 20 Jahre später zeugt Sohn (c) mit Mutter (a) ein Kind (d).

Rein Theoretisch wäre Sohn (c) ja der Vater und der Bruder. Der Vater (b) wäre Stiefvater und Großvater. (?)

Wie wäre hier die gesetzliche Regelung? Abgesehen von Inzest und und...

Ist Gott in der Lage etwas zu erschaffen dass mächtiger ist als er selber, denn wenn er dazu nicht in der Lage ist, ist er nicht allmächtig, aber sollte er es können ist er das auch nicht, da es dann etwas geben würde das mächtiger ist als er selber.

Angenommen es gibt Gott und dieser ist allmächtig wäre er in der Lage einen Stein zu erschaffen den er nicht hoch heben kann? Wenn er es könnte könnte er ihn ja nicht hoch heben und wäre nicht allmächtig, könnte er es nicht könnte er ja keinen Stein erschaffen den er nicht hoch heben kann und wäre ebenfalls nicht allmächtig gibt es überhaupt eine einleuchtende Antwort auf dieses Gedankenspiel?

Ich habe jetzt halb Russland eingenommen und dachte „Endlich ordentlich Rekrutenreserve“ aber da steht jetzt in den einzelnen Provinzen, „Basiswert für Wehrdienst (Nicht-Kerngebiet) -98%. Spiele als Deutschland und hab halt nach dem Krieg das Land angetippt was ich wollte und das sind jetzt „Koloniestaaten“ wie kann ich das ändern? Also das ich nicht diesen Malus von 98% hab.
Vielen Dank für schnelle Antworten

Hassen diese Leute damit nicht sich selbst? Alle waren doch mal Kinder.

Ich verstehe nicht wie Achilles die Schildkröte nicht einholen kann obwohl er ja schneller ist. Gleichen sich Geschwindigkeit von Achilles und Abstand zwischen beiden stets aus?

Ich werde wohl mein Fachabitur machen, danach würde ich gerne mein Abitur machen.

Studieren finde ich zwar cool, weiß aber nicht was ich danach machen soll. Pfarrer ist eigentlich ein cooler Job in dem man (zumindest in der heutigen Zeit) keine Probleme damit haben wird einen Job zu finden. Man trifft seine Mess-Vorbereitungen. Redet mit alten Menschen und man hilft Menschen. Ich muss dafür ja nicht gläubig sein, sondern einfach meinen Job machen. Wie es ein Arzt zum Beispiel macht, er macht einfach das was er in seinem Studium gelernt hat. So könnte er halt von den Methoden die er da anwendet auch nichts halten, er macht es aber einfach weil er es so gelernt hat. 🤷🏽

Eigentlich halte ich von Religionen gar nichts. Aber die Arbeit eines Pfarrers macht mich schon ein bisschen an. :D

Ist das also möglich, wenn ich weder auf körperliche noch auf Büro Arbeit stehe?

Ich bin getauft und zur Kommunion gegangen.

Also beim Allmachtsparadoxon geht es um die Frage, ob Gott einen Stein erschaffen kann, der so schwer ist, dass er ihn selbts nicht heben kann. Wenn er so einen erschaffen könnte, kann er ihn ja nicht heben -> Gott ist also nicht allmächtig. Aber wenn er so einen Stein nicht erschaffen kann, ist er auch nicht allmächtig.

Gibt es einen Ansatz welcher dieses Paradox umgeht, wie zb das der er den Stein leichter macht? Ich finde diesen Paradox einfach ziemlich spannend und würde gern einfach so wissen was ihr darüber denkt.

Auf diesen Paradox bin ich durch psycho pass gestoßen (zu empfehlen)

Eigentlich wird z.B. das Gegenteil eines Engels ja als Dämon, von Gott als Luzifer angesehen. Theoretisch, jedoch, könnte man auch sagen, dass ein Engel existiert, deswegen darf sein Gegenteil nicht existieren, was bedeuten würde, dass Engel kein Gegenteil besitzen. Dies, wiederum, würde diese Frage als nicht existent erklären, nicht?

Immer wieder, seit den jüngsten Tagen meiner Kindheit, sah ich ab und zu eine Zeichentrickserie, in der gerade ein sogenannter „Gegenteiltag“ in der jeweiligen Folge war. Und auch, wenn ich schon jahrelang nicht mehr TV schaue, fällt mir diese Frage beim Herumphilosophieren immer wieder ein:
Wenn bspw. der Protagonist, dieser Serie nun am Gegenteiltag, da er normalerweise das T-Shirt auf dem Oberkörper, und die Hose auf dem Unterkörper trägt, seine Hose auf dem Oberkörper und falsch herum, und sein T-Shirt auf dem Unterkörper und falsch herum trägt, wieso tut er dies?
Man könnte hier, je nach Definition, auch sagen, dass der Protagonist eine Hose trägt, deswegen darf er am Gegenteiltag keine Hose tragen.

Weiß jemand eine Lösung, auf dieses, in meinen Augen, paradoxe Verhalten des Gegenteils?

Kann man diese Frage ohne den Begriff "Paradoxon" zu verwenden beantworten?

Ziemlich verstörende Frage,aber wenn eine Schlange anfingen würde,sich selber von ihrem Schwanz aus aufzuessen,was würde Passieren? Ist ihr Schwanz IN einem ANDEREN Schwanz,oder wie? Kann diese frage mir seit Jahren vom Kopf nicht entfernen 0_0

Wäre es nicht ekelhaft, wenn ein 20 Jähriger noch an der Brust seiner Mutter nuckelt, oder diese aus einem Glas trinkt? Warum gelten aber bei der Milch von Kühen (die ja auch Muttermilch ist, aber fürs Kalb) anscheinend andere Massstäbe? Ist es nicht paradox das wir uns vor der Milch unserer eigenen Mutter ekeln, aber jeden Tag, ohne uns zu ekeln, Muttermilch von Kühen trinken?

Zoom tötet ja gelegentlich seine Zeit Relikte. Wenn sie aus der Vergangenheit kommen und sterben kann die Gegenwart ja nicht passieren. Also können sie nicht von dort aus kommen. Wenn sie aber aus der Zukunft kommen und sterben wäre das ja auch unpassend da man ja sonst in der Zukunft dem alten ich begegnet das einnen dann tötet. Aber woher kommen die dann ???

Nehmen wir an es gibt einen Gott. Gott ist ja allmächtig und kann ja bekanntlich alles.
Was ist wenn er einen so großen Stein erschafft den er nicht heben kann?
Also wäre Gott sozusagen nicht allmächtig.

Gibt es dagegen etwas einzuwenden?

Die Frage sagt schon alles. Wenn man das auf etwas antwortet, ist es dann ein "Kommentar" und damit Paradox, oder ist es kein Kommentar?

Guten Abend liebe Community,

ich habe im diese neue o2 Werbung gesehen und hab dazu im Internet recherchiert und da steht dass das Datenvolumen unendlich ist. Darunter verstehe ich zum Beispiel dass man nach einer Weile keine Nachricht mehr bekommt dass das Datenvolumen aufgebraucht ist was ich mir aber für schlappe 25€/Monat nicht vorstellen kann. Entweder ist das völlig Paradox oder ich verstehe es einfach nicht. Rechts steht unendliches Datenvolumen und links steht 1 GB Turbo Datenvolumen.

Das Zitat hab ich in einem Forum gelesen.

Ich möchte jetzt nicht wissen von wehm dieses Oben genannte Zitat kommt, eher würde mich Interessieren was es zu bedeuten hat bzw. Wie man es am besten Interpretieren kann? Wenn er von sich behauptet ständig zu lügen aber nun doch die Wahrheit spricht, lügt er ja trotzdem.. oder?

Bitte, dieses Zitat macht mich total Irre, kann es mir jemand erklären?

David Hilbert hat ja mal so ein Gedankenexperiment gemacht:
Stellt euch vor, es gibt ein Hotel mit einer unendlichen Zahl an Räumen und unten steht ein Nachtwächter (des Hotels). Eines nachts sind alle Räume des Hotels besetzt, mit einer unendlichen Zahl an Gästen. Dann kommt ein neuer Gast. Der Nachtwächter beschließt, den Gast in Raum eins zu Raum zwei, Raum zwei zu Raum drei zu verschieben und immer so weiter, also Raum n zu Raum n+1. Jetzt hat er genau einen leeren Raum für den neuen Gast.
Das ganze könnte er jetzt für jede endliche Zahl an neuen Gästen tun, aber was, wenn ein unendlicher Reisebus eintrifft? Der Nachtwächter beschließt, jeden Gast von Raum n zu Raum 2n zu verschieben, denn jetzt sind alle ungeraden Räume frei, also unendlich viele.
In seinem Paradoxon erwähnt Hilbert aber auch verschiedene Wege, auf die man Gäste aus unendlich vielen unendlichem Reisebussen unterbringen kann, zum Beispiel indem man jedem Gast den Raum der Nächten Primzahl hoch seiner Sitzplatznummer im Bus gibt, nachdem er jeden bestehenden Gast in Raum 2n geschickt hat. Sagen wir, die Busplatznummer ist i. Jetzt bekommen die Gäste aus dem ersten Bus Raum 3^i, aus dem zweiten Bus 5^i und immer so weiter. Jetzt aber meine Frage:
Wäre das nötig? Bei dem Problem mit dem einen unendlichen Reisebus war das doch auch nicht nötig, und unendlich ist ja immer gleich unendlich?

Gibt es sowas wie Allmacht? Man sagt ja z.B.: Gott ist allmächtig. Aber ist Gott so mächtig dass er einen Steinen erschaffen kann den nicht einmal er hoch gehoben bekommt? Wäre er denn noch allmächtig?

Es gibt ein Land namens Arkania dort müssen alle Bürgermeister in der Hauptstadt leben. Kein Bürgermeister darf in seiner Stadt leben. Wo lebt der Bürgermeister der Hauptstadt?

Hi, es gibt ja schon seit längerem den After Dark DLC. Bei einem Let's Player sah ich eine Mod, wo es nicht Nacht wurde. Er konnte allerdings über einen Schieberegler die Zeit verändern und somit Nacht machen. Weiß jemand wie diese Mod heißt? Danke im Voraus!

Logischerweise müsste es die Zeit schon immer gegeben haben oder ?
Andererseits ist es aber auch unlogisch .

Kann man das vielleicht noch irgendwie faktisch erklären oder driftet das zu sehr in den Bereich des unerklärbaren ab?😄

LG

Wie oben gesagt, das Spiel stürzt beim Start ab. Als erstes öffnet es sich in einem kleinen Fenster und schließt sich dann mit einer Fehlermeldung. Ich habe es auch schon neuinstalliert, aber nicht geht, obwohl es vorher einwandfrei funktioniert hat. Bitte um Hilfe!

Ich bin auf den Paradox Achilles und die Schildköte von Zenon gestoßen und fand diese unlogische Logik (=auch ein Paradox??) faszinierend. :D Hab dann noch welche gefunden wie Pinocchios Nase wächst dann, wenn er lügt. Was passiert aber wenn er sagt "Meine Nase wächst gerade" oder Unendlichkeit von Zeit und Raum: "Alles muss doch zu irgendeinem Zeitpunkt angefangen haben" - "Aber was war dann davor?"

Hallo zusammen,mich beschäftigt gerade sehr eine ziemlich paradoxe Frage...und zwar wie folgt: Wenn Gott allmächtig ist,kann er dann einen Felsbrocken erschaffen der so schwer ist das selbst er ihn nicht mehr hochheben kann?Wenn ja dann ist er doch nicht mehr allmächtig weil wenn er es wäre müsste er ihn doch hochheben können,aber genau so ist er doch nicht allmächtig wenn er so einen Fels nicht erschaffen kann!

Ich glaube mit der Frage kann zumindest ich mich länger beschäftigen als mit dem Fernseher O_O Bitte nur ernste Überlegungen!Eure Chacal<3

Denkt ihr, dass verschweigen zu lügen zählt? wenn ich zum Beispiel wichtige Fakten aus einer Geschichte weglassen würde, und sie dann anderst klingt würde ich dann lügen oder nicht? oder gibt es dafür einen anderen Ausdruck? Was denkt ihr??? verschweigen=lügen....?

Würde er an Hypochondrie leiden, würde er es sich nicht fälschlicherweise einbilden. Würde er nicht dran leiden, würde er sich eine Krankheit einbildet und wäre damit ja doch ein Hypochonder. Paradox?!

Hi,

Meine Frage lautet, wie kann man den Norddeutschen Bund in Victoria 2 gründen.

habe überall in Norddeutschland mit Preußen meinen Einfluss (sogar bei Sachsen, Hannover und Holstein).

Muss ich erst das Gebiet von Süddänemark anektieren?

Bitte um Rat