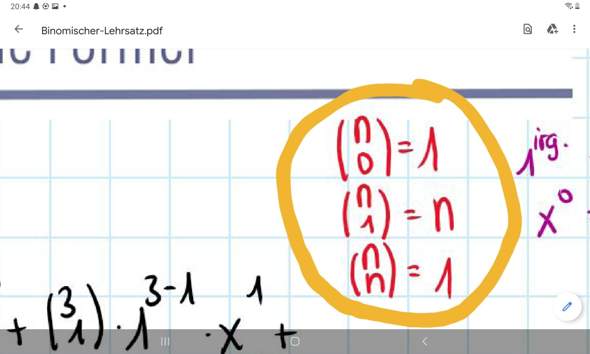
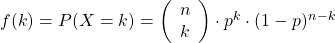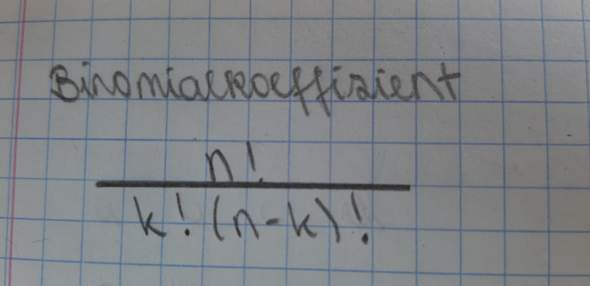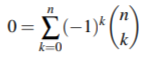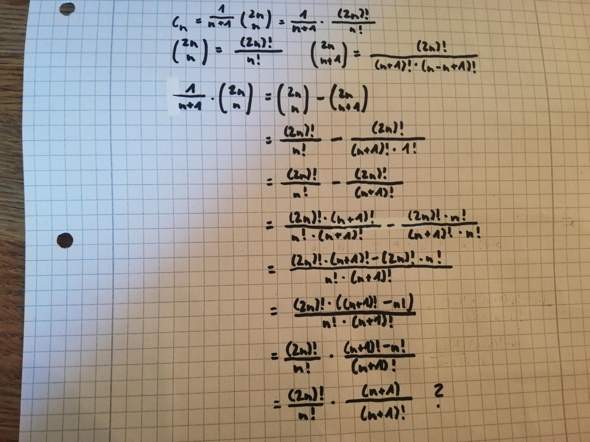Mathe frage binomialverteilung?
In der Jahrgangsstufe 12 besitzen 60 % der Schülerinnen und Schüler ein Smartphone. Berechnen Sie die Wahrscheinlichkeit, mit der man bei einer Stichprobe von 100 Schülerinnen und Schülern
a) genau 40,
b) zwischen 35 und 50,
c) mehr als 50,
d) weniger als 35
Ich habe a) ausgerechnet, erhalte aber 0,000024425 und weiß nicht, ob es richtig ist.