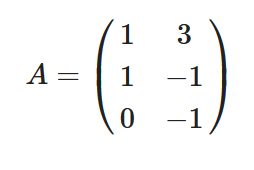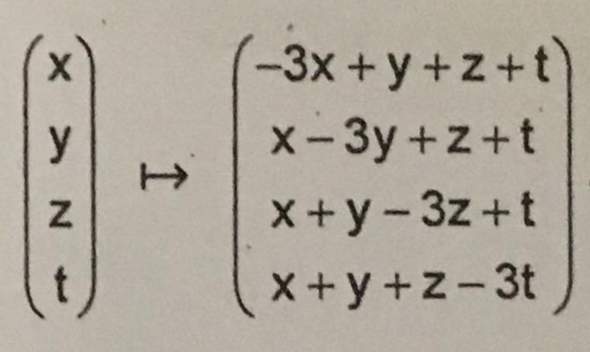Lineare Algebra – die besten Beiträge

Hallo! Ich habe nun schon ein paar Fragen zu Gerschgorin-Kreisen gestellt, jedoch hab ich immernoch offene Stellen bei denen ich Aufklärung benötige...

Ich habe also nun die Zeilen- und Spaltenkreise berechnet. Was genau nun? Ich wurde sagen: Vereinigung der Spaltenkreise bilden und die Vereinigung der Zeilenkreise bilden. Nun diese Beiden Vereinigungen schneiden und ich habe eine Menge in welcher die Eigenwerte liegen.

Möchte ich nun genauere Aussagen treffen bilde ich jeweils den Schnitt des ersten Spaltenkreises mit dem ersten Zeilenkreises. Dann den Schnitt des zweiten Spaltenkreises mit dem zweiten Zeilenkreis. ... Dann den Schnitt des n-ten Zeilenkreises mit dem n-ten Spaltenkreis. Jetzt habe ich diese n-vielen Schnitte und schaue mir an welche mit welchen disjunkt oder eben nicht disjunkt sind. Sind nun m- viele dieser n- vielen Schnitte nicht disjunkt liegen in der Vereinigung dieser m-vielen Schnitte genau m-viele Eigenwerte. Richtig?!?!? Und wie ist es mit der Algebrischen vielfachheit? Angenommen es überlappen sich 3 Kreise und die Eigenwerte sind a, b und nochmal b und c. In der Vereinigung dieser 3 Kreise liegen also 3 Eigenwerte. Kann es sein, dass a, b und wieder b in der Vereinigung liegen oder nicht, da b=b?

Vielen Dank und LG MAx Stuthmann

Hallo! Ich habe folgendes Problem gegeben...

z.z., dass....



eine Determinantenform ist.

Wie zeigt man so etwas? Ich habe den Verdacht, dass man hier irgendwelche Axiome/Eigenschaften nachweisen muss, finde aber zurzeit nirgends ordentliche Quellen, welche Eigenschaften das wären.

Danke.

http://www.poenitz-net.de/Mathematik/7.Analytische%20Geometrie/7.8.A.Kugeln.pdf

Hat jemand vielleicht eine Idee, wie man die Aufgabe 6 lösen kann? Ich komme einfach nicht auf einen brauchbaren Ansatz.

Der Schnittkreis befindet sich in der x-y-Ebene, welche durch die Gleichung E: z=0 beschrieben wird. Zudem kennt man den Mittelpunkt (0|0|0) und den Radius (r'=7) des Schnittkreises. Über die Beziehung r'²=r²-d² lässt sich der Radius der Kugel jedoch nicht bestimmen, da r (Kugelradius) und d (Abstand Kugelmittelpunkt zur Ebene) unbekannt sind.

Eine andere Idee war jetzt, den Schnittkreis in eine Kugel zu "überführen" und diese dann von der eigentlichen Kugel abzuziehen. Es sollte sich die oben erwähnte Schnitt- bzw. Trägerebene ergeben. Jedoch scheint dieser Ansatz nicht der richtige zu sein.

Mein Problem: Was sagt mir der Punkt A(8|15|10)? In Geogebra konnte ich sehen, dass er auf der Kugelfläche liegt. Was soll ich jedoch damit anfangen? Ich könnte höchsten den Abstand des Punktes zur Ebene bestimmen - aber was bringt das?

(Die Lösung ist anbei des PDF Dokuments, jedoch ohne Lösungsweg.)

Moin! Ich hatte jetzt schon Analysis 1 und 2, Lineare Algebra 1 und 2 und Numerische Mathematik. Frage mich was in Analysis 3 so für Themen behandelt werden...

Danke und Lg max

Hi, könnt ihr mir vielleicht sagen, wieso diese Matrix den Rang 2 haben soll. Ich dachte es gilt Zeilenrang= Spaltenrang, wieso ist der Rang nicht 3?

Und ich wollte euch auch noch fragen, ob ich nicht für die Basis von im(f) auch einfach die beiden Spaltenvektoren als Basis verwenden dürfte ((1,1,3)^T,(3,-1,-1)^T), weil in den Lösungen auch hier etwas umständlicher vorgegangen wurde.

VG:)

Hallo

Ist die folgende Matrix mit Gaus ohne Pivoting lösbar?

Pivoting bedeutet ja, dass man die Zeilen so tauscht, dass das größte Element der Spalte (jeweils unter den Diagonalelementen) mit den Diagonalelement der Spalte getauscht wird und somit das neue Pivotelement wird.

Hier mal an dem Bsp ausgeführt:

Nun könnte ich per Rückwärtseinsetzen lösen

Nun haben wir aber nur das Gauß Verfahren und nachdem ich etwas umforme folgt

Wie würde es nun ohne Pivoting weitergehen? Geht es überhaupt weiter?

hallo zsm, kann mir bitte jemand bei der Aufgabe 7 helfen? Ich habe es zum Teil gelöst bin mir aber sehr unsicher.

7c) E: x= (0|0|2) + r * (1|1|1) + s * (-1|-1|1)

7d) E: x= r * (0,5|0,5|0,5) + s * (-0,5|-0,5|0,5)

Mich interessiert die Aufgabe 7d am meisten, da gefragt nach Spannvektoren gefragt ist, welche nicht das vielfache von E sein soll. Bedeutet es, dass die Zahlen einfach kleiner sein sollen statt größer? Ich würde um eine ausführlichere Erklärung sehr dankbar sein.

7a fand ich zu schwer, ich habe gar keine Ahnung wie die Lage ist, bzw was man hier genau tun soll.

Hallo,

sagen wir mal ich habe eine 3x2-Matrix, nennen wir sie A.

Für den Kern muss ja Ax=0 gelten. Ist das dann ein Vektor x derat, dass x=(u,v,w)? Wie geht das in diesem Fall?

Hallo, alle. Ich hätte eine Frage bezüglich einer Matheaufgabe. Wäre bitte jemand so nett und würde mir helfen? Sie lautet so:

"Gegeben ist f, ein Endomorphismus von IR^4, das folgendermaßen definiert ist:

f ist eine Projektion auf eine Hyperebene, gefolgt von einer Homothetie. Frage: Was ist das homothetische Verhältnis?" In anderen Worten, um wie viel wird hier vergrößert/verkleinert?

(Falls dies hilft, man kann die vierte Gleichung oben im Bild mithilfe von einer Linearkombination der anderen drei bekommen.)

Könnte mir jemand bitte helfen? Ich weiß hier leider nicht weiter…

Vielen Dank im Voraus!

Bei L' steht "P(2)(X²-1)", was genau heisst das? Bei L steht einfach "P(X-2)", dass heisst, dass man im Polynom einfach die "X" durch "X-2" ersetzt, richtig? Also Wenn P(X) zb das hier wäre: P(X) = 1 + 2X + 3X², dann wäre P(X-2) = 1 + 2(X-2) + 3(X-2)²

Aber was soll das P(2)(X²-1) bedeuten? Wie würde P(2)(X²-1) für P(X) = 1 + 2X + 3X² aussehen?

Guten Tag liebe Gemeinde,

ich bin gerade an der Berechnung des Flächeninhaltes eines Polygons mit Hilfe des Kreuzproduktes. Um genau zu sein, geht es hierbei um dieses Polygon.

Es handelt sich hierbei um Vektoren aus dem R^2. Laut Beschreibung ist das Kreuzprodukt im R^2 ein Skalar, welcher den Betrag des Flächeninhaltes angibt. Nun soll ich ebenfalls die Durchlaufrichtung beachten, also erst einmal von A - F und anschließend von F-A. Laut der Berechnung des Kreuzproduktes bewirkt die Vertauschung der Vektoren ein Vorzeichenwechsel. Nur stellt sich mir die Frage, wie ich diesen Flächeninhalt mit Hilfe des Kreuzproduktes berechnen kann. Kann mir bitte jemand einen Denkanstoß geben?

Liebe Grüße

Hi,

ich bin gerade mit einer Aufgabe beschäftigt und frage mich, was diese Schreibweise bedeutet.

Kann mir jemand weiterhelfen? Die Aufgabe befindet sich direkt im zweiten Bild, falls ein Zusammenhang benötigt wird. Danke im Voraus.

Hallo. Kann jemand mir die Hinweise für die 3te Aufgabe. Wie kann man die Schnittgebilde von 4-dimensionale Raum bestimmen. Ich habe geprüft wenn man E1=E2 stellt ergibt eine eindeutige Lösung. Was bedeutet das?

Danke

Hey Leute!

Kann mir bitte wer sagen, was mit diesem C^2[0,2pi] gemeint ist? Ich nehmen an, dass es sich nicht um das Zeichen für den Komplexen Zahlenraum handelt?

Danke!

Kann mich evtl. jemand auf Quellen verweisen, die erklären, wie man solche Aufgaben löst?

Kann mir einer erklären, warum bei (iii) der Umkreis so ist wie er ist ?
Ich habe mir gedacht, dass eben Betrag von z der Radius ist und deswegen eben alles im roten Umkreis. Mein Problem ist, dass ich nicht verstehe, warum er bei -4 und +1 liegt. Im Betrag wurde der Zahl doch das genaue Gegenteil gegeben. Warum ist das nun so ?

Müsste man dem LGS entsprechend nicht für x2 bei q=0 eine x-beliebige Zahl einsetzen können. Warum orientiert sich die Lösung für q ungleich Null an s und nicht am Lgs, wie kommt man auf den Vektor, für den man keine Fallunterscheidung braucht und gibt es irgendein naheliegenden Grund, warum man hier erst eine Fallunterscheidung für q=0 bzw q ungleich Null vornimmt und nicht gleich nach einen passenden Vektor sucht?

Ich weiß, dass sind eine Menge Fragen (no pun intended) auf einmal. Ich wäre auch für Teilantworten sehr dankbar!

Hallo liebe Community,

es geht um die folgende Aufgabe:

Kann mir jemand sagen, welche Determinanten Umformregeln ich hier sinnvoll anwenden kann?

Eigentlich dachte ich, die Umformregeln bei Determinanten ganz gut drauf zu haben, aber hier macht doch weder das Ausklammern noch das Addieren/ Subtrahieren einzelner Zeilen bzw. Spalten Sinn.

In der Zeit hat man doch schon ganz schnell über den Laplace'schen Entwicklungssatz und dann die Sarrus'sche Regel die Determinanten berechnet...

Springt Euch eine Regel ins Auge, deren Anwendbarkeit Sinn macht?

Besten Dank im voraus!

Grüße carbonpilot01

Sorry wenn ich so oft nachfrage, ich verstehe es aber einfach nicht. Diese Aufgabe soll wohl sehr einfach sein, ich verstehe aber trotzdem nicht wie sie geht :(((

Ich hätte mir folgendes gedacht: Um die Abbildungsmatrix zu bestimmen, schau ich mir einfach die Bilder der Basisvektoren an. Leider verstehe ich nicht so ganz, was z denn jetzt sein soll. Einerseits wird z bei der Definition von IQ(3wurzel(5)) verwendet, andererseits ist das jetzt aber auch ein Element von IQ(3wurzel(5)). Das sind doch hoffentlich zwei unterschiedliche z, oder? Wenn z ein Element aus IQ(3wurzel(5)) ist, dann bedeutet das ja, dass z das hier ist:

 α,β,γ€IQ. Danach wird aber erst IQ(3wurzel(5)) als Vektorraum über IQ gesehen, dann wird die Abbildung Tz Endomorphismus vom IQ-Vektorraum IQ(3wurzel(5)) definiert, und wenn das z so wäre, wie ich es gesagt habe, dann wäre es ein Skalar, also kann das mit dem z ja schonmal nicht hinhauen, weil z ja kein Element aus IQ ist somit kein Skalar sein kann. Ich checke einfach nicht, wie dieses z denn nun aussehen soll. Das x ist ein Element aus dem Vektorraum, also ist x ein Vektor, der somit wiefolgt aussieht:

Wenn x jetzt ein Basisvektor ist, dann wären zwei Unbekannte 0, die übriggebliebene wäre 1. Und was nun? Ich verstehe einfach nicht, wie so ein z aussieht und was dann in der Abbildung mit den x und z passiert, kann mir das jemand erklären, danke :(

Ich bin mir nicht mal sicher, ob ich die Aufgabe richtig verstehe. In welcher Relation steht der Index I zu der Teilmenge des Vektorraums? Ist das ein Vektor oder eine Zahl? Wenn ai ein Vektor ist und nicht der Nullvektor und so groß ist wie die Summe der restlichen Vektoren, so kann ich durch subtrahieren den Nullvektor ausrechnen, ist das der Ansatz? Für Erklärungen oder gleich ein Beweis wäre ich sehr dankbar!!