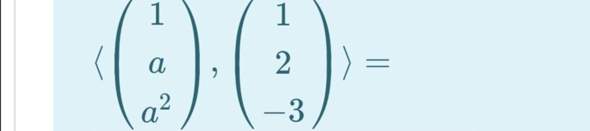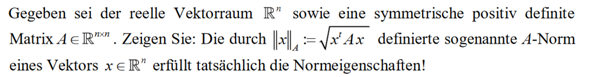Lineare Algebra – die besten Beiträge

Ich verstehe einfach nicht, was dieses "Wir setzen V/U = V/~" bedeuten soll und wie diese Operationen definiert sind. Ich habe herausgefunden, dass V/~ für die Menge der Äquivalenzklassen steht. [v]~ steht für die Äquivalenzklasse von v und die Menge besteht aus allen w€V, für die ein u€U existiert, sodass w+u=v, also:

[v]~ = {w€V | ∃u€U: w+u=v}

So, ich hab mir das jetzt einfach mal wie folgt vorgestellt: Sagen wir mal, U ist ein echter Unterraum von V und V sei jetzt einfach mal IR³. U ist jetzt einfach mal IR², also ein echter Unterraum von V, man könnte sich U also quasi wie die xy Ebene vorstellen im IR³. Jetzt sind zwei Elemente aus V (also IR³) genau dann in einer Relation, wenn sie in einer Ebene liegen, die parallel zur "U-Ebene" ist. Somit ist die Menge [v]~ für jedes v€V unendlich groß (richtig?).

V/~ ist nun also einfach die Menge dieser Äquivalenzklassen. Aber was heißt dieses "Wir setzen V/U = V/~"? V ohne U ist erstmal bloss eine Menge von Vektoren, V/~ hingegen ist eine Menge von Mengen mit Vektoren, wo macht das also Sinn??

Außerdem, wie kann ich mir diese Operationen denn genau vorstellen? Hier werden auch wieder zwei ganze Mengen addiert und nicht einfach zwei beliebige Elemente, ich checke es einfach nicht. Wäre jemand so nett und erklärt mir das in einfachen Worten? :(

Wir nehmen an, dass die drei Vektoren, welche die Grundfläche dieser Pyramide bilden, bekannt sind. Wir nehmen auch an, dass wir das Volumen des Tetraeders kennen. Mit welcher Formel kann ich nun alle mögliche Koordinaten der Spitze des Tetraeders ausrechnen?

Hallo,

Es seien A eine Menge, A⊆B und   x ∼ y : <=> ( x ∈ A ∧ y ∈ B ) ∨ x = y

Dass ∼ eine Äquivalenzrelation auf A ist, ist mir klar. Aber wie kann ich die Äquivalenzklassen bestimmen?

Frage steht oben, sagen wir ich habe eine 3x3 Matrix, dazu die Eigenwerte und Eigenvektoren. Was sagen diese nun genau aus und was kann ich nun mit dieser speziellen Matrix der Eigenwerte anstellen bzw die Eigenvektoren?

stimmt das, dass die Eigenvektoren eine orthogonalbasis bilden?

und was passiert da bei einer hauptachsentransformation, das geht dich mit diagonalmatrizen besonders einfach, die nur werte an der Diagonale haben. Wieso ist das so?

danke

Hallo zusammen!

Ich habe eine Frage und zwar zur Berechnung einer Abbildungsmatrix das jedes Element einer 2x2 Matrix auf seine transponierte abbildet bezüglich der Standardbasis Basis B (sorry für die nicht ganz übersichtliche Darstellung):

 1 0    0 1   0 0   0 0
 0 0 ,  0 0,  1 0,  0 1 

Meine Gedanken dazu bis jetzt:

Also wie ich es verstanden habe, muss ich eine Abbildungsmatrix erstellen, welche mir die Matrix: (a11, a12, a21, a22) auf (a11, a21, a12, a22) abbildet anhand der Basis B?

Aber wie mache ich das nun?

Vielen Dank für eure Hilfe!!!

Grüsse und noch einen schönen Abend!!!

Hi

Ich habe hier folgende Aufgabe vor mir liegen...

Wie geht man da genau vor? Im Internet habe ich dazu nichts gefunden oder ich habe wohl falsch gesucht. Was eine lineare Abbildung ist ist mir klar. x ist wohl definiert also x1 und x2 von R^2 sind da wohl definiert. Erhält man dann so eine Matrix daraus? Aber was ist mit dem Rest der Aufgabe gemeint? Bzw. habt ihr Lösungsansätze?

Freue mich auf Antworten :)

LG

Wenn ich folgendes Skalarprodukt ausrechne, komme ich auf eine quadratische Funktion nach deren Auflösung ich zwei Werte für a erhalte. Ist in jenem Fall, das Skalarprodukt nicht definiert?

Hallo, ich habe hier eine Matheaufgabe und ich habe das eingekreiste Symbol noch nie gesehen. Vielleicht kann mir jemand helfen.

Hallo, könnte mir jemand vllt. mit folgender Aufgabe helfen. Bei U dürfen die Koordinaten nicht alle positiv oder negativ sein. Gibt es aber ein Systematisches Verfahren wie ich eine Basis von so einer Gleichung ermittle? Mein ansatz ist, mir evtl. die lineare hüllen anzusehen aber darf ich annehmen das hier die kanonische basis verwendet wird?

Danke

Hey leute...das ist mein erstes Semester des Informatikstudiums und ich tue mir sehr schwer beim mitkommen. Gibt es einen online Kurs oder ein sehr eifaches Buch? Jetz aber zu den Aufgaben...ich konnte das erste Gleichungssystem lößen jedoch komme nun nicht weiter....

Der Frage sind zwei Bilder beigefügt. Beim oberen Bild wird festgehalten, dass R auf R abgebildet wird durch R->R, wenn ich der Argumentation richtig folge. Beim zweiten Bild kommt ein x vor bei Q X Q. Was bedeutet dieses x?

Falls eine Lösung existiert ist es zumindest möglich, dass diese bei einem überbestimmten Gleichungssytem eindeutig ist, meiner überlegung nach ja, stimmt das? Bei einem unterbestimmten ist es logischerweise unmöglich.

Was bedeuted das "hoch T" über dem Tupel? und wie würde man b) geometrisch inerpretieren- etwa R3 ohne den positiven Quadranten oder wie das in R3 heißt?

es heißt ja immer, dass man lineare algebra für zum beispiel elektrotechnik, informatik, finanzmathematik, mathematik benötigt. Aber kann mir mal wer praktische anwendungen nennen? Nicht so oberbegriffe wie ich schon angeführt habe. Würde mich mal interessieren, da auf der uni immer sehr viel wert auf theorie aber wenig wert auf praxis gelegt wird, würden mich mal anwendungen in der praxis interessieren.

Grenzkosten mathematisch ausgedrückt ist ja so:

K`(x) = y (Erste Ableitung der Kostenfunktion)

Aber wie ist es bei einen Gewinnrückgang?

Ich habe folgende Aufgabe gegeben:

In unserem Skript steht:

Daher muss ich diese 3 Eigenschaften für die A-Norm zeigen.

Die ersten beiden waren kein Problem, aber bei der Dreiecksungleichung komme ich gerade einfach nicht weiter.

Hallo!

Ich studiere Mathe und bin gerade im zweiten Semester. Das Semester neigt sich dem Ende hin und wir schreiben bad Klausuren. Wir haben im ersten Semester keine Klausuren geschrieben und schreiben nun Analysis 1+2 und Lineare Algebra 1+2. Bedeutet Stoff von zwei Semestern! Wir haben im ersten Semester einer Probeklausur in Analysis 1 geschrieben, bei der ich relativ schlecht abgeschlossen habe. Verwundert mich aber nicht, denn es hat von über 100 Leuten nur einer theoretisch bestanden und ich habe mich ehrlich gesagt nicht soo richtig gut vorbereitet. Vor etwa einem Monat haben wir eine LinA Probeklausur geschrieben die mir relativ leicht viel.

Also. In einer Woche ist Vorlesungsfreie Zeit. Bedeutet in ca. 5 bis 6 Wochen schreibe ich Analysis und dann nach weiteren 3 bis 4 Wochen Lineare Algebra.

Mein Plan:

Erst das Skript von vorne bis hinten durcharbeiten, dann vergangen Übungszettel durcharbeiten (Musterlösungen studieren und selber bearbeiten) und dann Klausuren von Vorjahren und anderen Unis bearbeiten.

Natürlich gibt es nicht die EINE Lernstrategie die für jeden am besten ist. Trotzdem würde ich gerne nach Tipps fragen! Wäre cool, wenn ihr vielleicht aus Erfahrungen berichten könnt und/oder sagen, ob ihr Teile zu meinem Plan hinzufügen oder vielleicht ändern würdet.

Danke!

LG Max Stuthmann

Hey, wenn ich 2 Punkte P(p1,p2) und Q(q1,q2) habe und daraus eine Gerade Bilde, erhealte ich ja z.B. g: x = (p1,p2)^t +r (q1-p1, q2-p2)^t , r € R
Wie berechne ich den Abstand eines punktens (x1,x2) von dieser geraden.
Also wie kann ich das allgemein berechnen, so dass am ende eine "Formel" raus kommt?

Hallo

Ich komme bei dieser Aufgabe nicht weiter. Kann mir das vielleicht jemand erklären? Und kann mir jemmand sagen was die Eigenwerte mit einer Population machen?