Was bedeutet diese Schreibweise (lineare Abbildung, Polynome)?
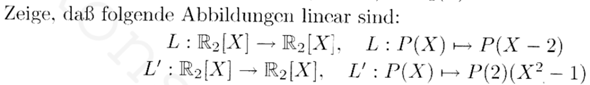
Bei L' steht "P(2)(X²-1)", was genau heisst das? Bei L steht einfach "P(X-2)", dass heisst, dass man im Polynom einfach die "X" durch "X-2" ersetzt, richtig? Also Wenn P(X) zb das hier wäre: P(X) = 1 + 2X + 3X², dann wäre P(X-2) = 1 + 2(X-2) + 3(X-2)²
Aber was soll das P(2)(X²-1) bedeuten? Wie würde P(2)(X²-1) für P(X) = 1 + 2X + 3X² aussehen?
2 Antworten
Bei P(X - 2) wird beim Polynom P(X) das X durch X - 2 ersetzt.
Bei P(2)(X² - 1) wird zunächst beim Polynom P(X) das X durch 2 ersetzt, was dann P(2) liefert. Und dieses P(2) wird dann mit (X² - 1) multipliziert. (Der Malpunkt wird ja in der Mathematik häufig weggelassen, wenn klar ist, das multipliziert wird.)
Beispiel:
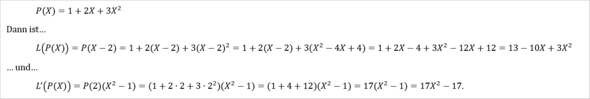
Wenn da sowas wie 17(X² - 1) bzw. 17X² steht, wunderst du dich doch wahrscheinlich auch nicht, was da steht, sondern erkennst, dass damit 17 ⋅ (X² - 1) bzw. 17 ⋅ X² gemeint ist, oder? Und genauso ist es hier, dass P(2)(X² - 1) gleich P(2) ⋅ (X² - 1) ist.
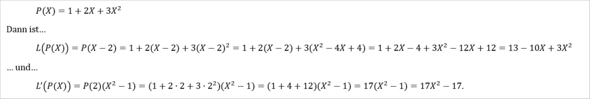
In der Tat eine seltsame Schreibweise... Möglicherweise ist damit
P(2) * (X² - 1) gemeint. Dann wäre in deinem Beispiel
L'(P(X)) = P(2) * (X² - 1) = 17 * (X² - 1).