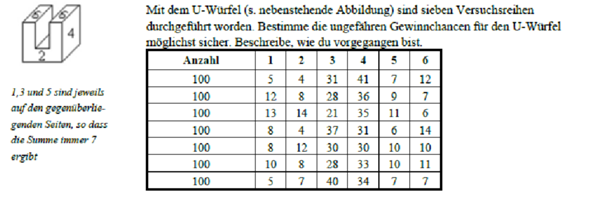
Wahrscheinlichkeit U-Würfel?
Moin Leute, ich habe eine Hausaufgabe welche ich leider nicht komplett verstehe. Muss ich quasi die relativen Wahrscheinlichkeiten für die 1,2,..6 herausfinden oder was ist genau verlangt. Wie gehe ich am besten vor ? Und dann soll ich die Ergebnisse erklären. Ich hoffe ihr könnt mir weiterhelfen