Irrationale Komplexe Zahl?

Hallo! Ich würde gerne wissen, ob es irrationale Komplexe Zahlen gibt, und wenn ja, was eine ist.

Ist eine Irrationale Komplexe Zahl einfach dann so eine, wenn sie nicht als Bruch zwei Gaußscher Zahlen geschrieben werden kann? Oder gibt es da eine andere Definition?

Und wenn ich weiß, was eine irrationale Komplexe Zahl ist, kann ich dann einfach eine irrationale Imaginäre Zahle nehmen, und dann durch i teilen, um eine Irrationale Zahl zu erhalten?

Danke!

Answer 1

[Willibergi]

Per üblicher Definition nicht.

Die reellen Zahlen enthalten die rationalen Zahlen und die irrationalen Zahlen. Alle Zahlen, die zu den reellen, aber nicht zu den rationalen Zahlen gehören, sind irrational.

Die komplexen Zahlen sind dann eine Obermenge der reellen Zahlen. Irrationale Zahlen sind aber per Definition reell.

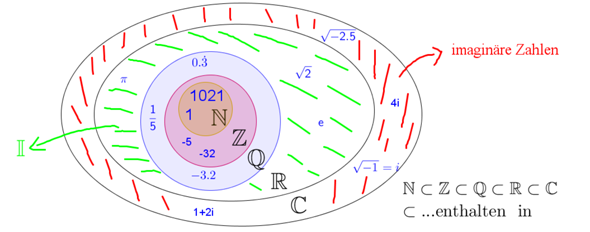
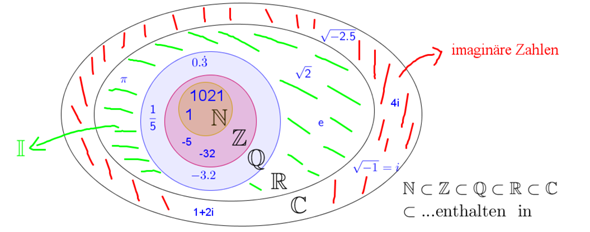
Quelle: https://3.vobs.at/maturawiki/index.php/Zahlenmengen

Hier in grün die irrationalen Zahlen. IR wird gebildet aus der blauen Menge (den rationalen Zahlen) und der grünen Menge (den irrationalen Zahlen).

Woher ich das weiß: Studium / Ausbildung – Studium Mathematik

Comments

[NeilderMensch]

Danke!

Gibt es trotzdem so etwas ähnliches?

[Willibergi]

@NeilderMensch

Es gibt in der Mathematik nichts, was es nicht gibt, weil man sich alles definieren kann. Eine übliche Definition sind "irrationale komplexe Zahlen" aber nicht.

[NeilderMensch]

@Willibergi

Danke! Dann definiere ich es mir schnell:

Ich habe die ganzen Gaußschen Zahlen, und eine Irrationale Komplexe Zahl ist eine Zahl, die nicht als Bruch zweier ganzer Gaußscher Zahlen geschrieben werden kann.

Das wäre eh mein nächster Schritt gewesen!

Vielen Dank!

[Willibergi]

@NeilderMensch

Gerne.

Answer 2

[mihisu]

Die Menge der irrationalen Zahlen ist eine Teilmenge der komplexen Zahlen.

$\underbrace{\mathbb{R}\setminus\mathbb{Q}}_{\text{irrationale Zahlen}}\subset \underbrace{\mathbb{R}}_{\text{reelle Zahlen}}\subset\underbrace{\mathbb{C}}_{\text{komplexe Zahlen}}$

Da also jede irrationale Zahl insbesondere immer auch eine komplexe Zahl ist...

Ja, es gibt irrationale komplexe Zahlen. Jede irrationale Zahl ist eine solche irrationale komplexe Zahl.

Answer 3

[Jangler13]

In diesem Paper werden rationale komplexe Zahlen definiert, als Zahlen die man als Bruch zweier Gaußische Zahlen darstellen kann. Irrationale komplexe Zahlen sind dann die komplexen Zahlen, die keine rationale komplexe Zahl sind.

https://www.jstor.org/stable/1988849?seq=1

Diese Definition gilt aber NUR in dem Paper, da im allgemeinen nicht über "irrationale komplexe Zahlen" geredet wird.

Woher ich das weiß: Studium / Ausbildung – Mache derzeit meinen Mathematik Master

Comments

[NeilderMensch]

Danke! Ich habe sie gerade eh selber definiert.