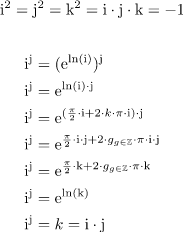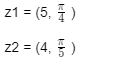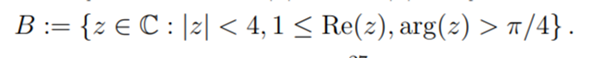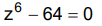Wie definiert man x/0?
Hallo!
Ich hätte eine Frage: Wie kann ich x/0 Definieren?
Unendlich als Lösung lasse ich mal raus, da es da zuuu viele Probleme gäbe.(Außer wenn 1*Unendlich Kleiner ist als 2*Unendlich. Glaube ich schon, weiß ich aber nicht. Und es gäbe immer noch Probleme.)
Ich würde ja sagen(Wenn j eine Komplexe Zahl ist):
x/0 = xj
Aber: 0/0 = 0j = 0
Und 0*x ist immer 0. Also würde ich doch sagen, dass 0/0 = Alles
Und damit würde ich sagen: 1=2=3=4=5=...
Also könnte ich ja sagen, 0/0 = g
Aber ich müsste auch j*0=x>|<0 Definieren. Aber alles mal 0 ist doch 0.
Und wenn das alles gehen würde gäbe es immer noch 1 Problem:
Ich kann Brüche erweitern und kürzen:
1/0 = 2/0 = 3/0 = ...
Also definiere ich nur eine Komplexe Zahl j:
x/0 = j
Aber dann wäre es doch: 1/0 = 2/0 | *0
1=2=3=4=...
Und ich würde sagen, dass j = 2j. Und da gäbe es auch Probleme:
Durch j teilen würde nicht gehen, da 1 sonst 2 wäre.
Und ich würde auch sagen, dass j = 0 ist, wodurch x/0 = 0 wodurch der Kehrwert das selbe wäre, wodurch ich sagen würde, dass 0 = 1.
Kann man das überhaupt definieren? Und wenn ja, wie?