Binomische Formel wird bei Wurzel vernachlässigt?

So, wir haben heute in der Schule eine Aufgabe von einem Test verbessert und ich sehe nicht ein, wie mein Lehrer das oben ( rechts jetzt) behaupten kann. Wie ich die Sache sehe, müsste doch die 1. Binomische Formel berechnet werden. Ich mein klar, mit Wurzel und hoch 2 löst sich auf, aber die binomischen Formeln haben doch Vorrang, oder nicht?
Ich verstehe es einfach nicht.
Schönen Abend euch noch,
Ta777784
4 Antworten
hier

hat jemand einfach nur die 2 vergessen beim a . Den Exponenten
es ist immer richtig dieses : ( wurzel(irgendwas) )² = irgendwas . Und man muss das irgendwas nicht erst ausrechnen oder zusammenaddieren . Man kann es sofort hinschreiben
( wurz(3x + 7 + 4x) ) ² = 3x+7+4x = 7x+7
.

und man muss eben aus wurz² nicht erst das machen . Die binom auszurechnen ist doppelte , unsinnige Arbeit . Denn am Ende MUSS 1+a² dastehen
.
Aber Achtung : Viel interessanter ist es , wenn man das

vorliegen hat . Hier sollte man erkennen , dass man eine ausgerechnete binom unter der Wurzel hat und man deshalb !!! durchaus die Wurzel ziehen kann
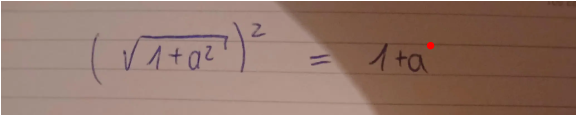
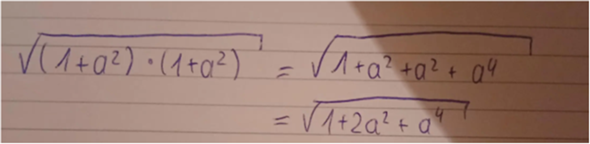
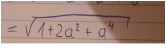
Ich hätte die Aufgabe als Gleichung verstanden und erhalte dann a1= 0 und a2= 1 als Ergebnis. Wahrscheinlich war das so aber nicht gemeint.
Die Rechnung in der ersten Zeile ist einfach falsch.
Die Binomischen Formeln haben gar keinen »Vorrang«. Man kann sie anwenden, wenn man sie sieht, muss aber nicht. Eine Wurzel zum Quadrat ist immer einfach das, was unter der Wurzel steht (Radikant). Danach kann man immer noch die binomische Formel rückwärts anwenden auf 1+a^2 = (1+a)(1-a). Vielleicht verwechselst du
wurzel(1+a^2)^2 und
wurzel((1+a^2)^2) = wurzel((1+a^2) * (1+a^2))
Ich war ( bin) eben der festen Überzeugung, dass das nicht geht, speziell eben bei Summen/Differenzen.
Außerdem versteh ich jetzt auch nicht ganz weshalb da bei der letzten Zeile deiner Erklärung nun 2 Klammern nach „Wurzel“ kommen. Ich seh zwischen den beiden eben einfach keinen Unterschied.
Mathe ist wohl auch nicht so meine größte Stärke, bin da etwas schwer von Begriff.
Sorry, aber jetzt muss ich dich auch korrigieren:
binomische Formel rückwärts anwenden auf 1+a^2 = (1+a)(1-a).
Das ist falsch.
(1+a)(1-a)=1-a² und nicht 1+a²
Ja, okay, das ist mein Fehler, hab ich wohl vergessen mitabzuschreiben, macht die Sache da aber auch nicht besser. Weil es ja eher darum geht, warum mein Weg von der ausgeklammerten binomischen Formel nicht zu 1+a^2 führt.
Huch, natürlich, danke. Keine Notwendigkeit, für eine Korrektion um Entschuldigung zu bitten.
Letztendlich kannst du das wieder als binomische Formel (1+a²)² schreiben und dann die Wurzel ziehen.
Man kann direkt die Wurzel ziehen, der Umweg ist nicht nötig.
Wurzel aus (3+4)² ist 7, warum sollte man Wurzel aus (9+24+16) stattdessen rechnen?
Aber wenn es doch nur ein Umweg ist, dann müsste mein Ansatz doch am Ende auch zu demselben Ergebnis führen, tut es aber eben nicht.
Doch, wenn du die ausmultiplizierte Form wieder als Quadrat schreibst.
Die binomische Formel kann man am Ausdruck unter der Wurzel anwenden, aber hier ist es absolut nicht notwendig, wie dir auch die anderen Antworten zeigen.
Ich dachte, wenn im Radikanden eine Summe ist, dann gehen die binomischen Formeln vor und nicht das Auflösen der Wurzel. Außerdem hab ich ja auch ( hoffe ich mal, grundsätzlich richtig) die Mutiplikationsregel angewandt. Warum wird somit das Ergebnis verändert?