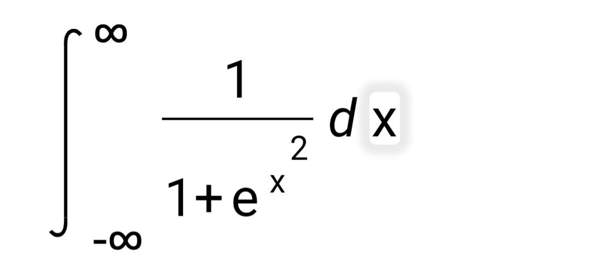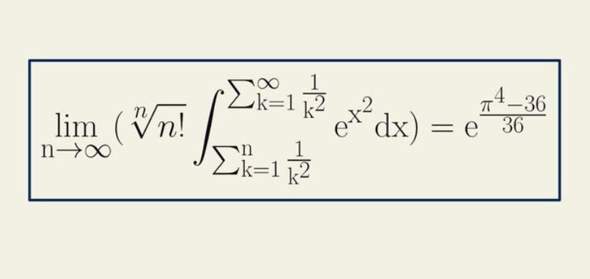Höhere Mathematik – die besten Beiträge

Hallo!

Ich kenne mich noch nicht sehr gut mit den Sedenionen aus, da ich erst noch die Quaternionen lerne. Aber ich habe trotzdem mal auf Wikipedia danach geguckt, und da steht, dass es Sedenionen gibt, für welche gilt:

p, q ≠ 0

pq = 0

Also wenn ich zwei Sedenionen ungleich null habe, und sie multipliziere, kommt 0 dabei raus. Ich denke auch, dass das Sinn macht, wenn man sich die Multiplikationstabelle anguckt. z.B. die Sedenionen e3+e10 und e6-e15 miteinander multipliziert ergeben null. Ich kenne mich mit den Rechenregeln bei den Sedenionen noch nicht so gut aus, aber würde dass nicht heißen, dass:

p, q ≠ 0

pq = 0 | /q

p = 0/q | ^-1

p^-1 = q/0

Kann man mit den Sedenionen durch null teilen??? Ich denke nämlich auch, dass es nicht einfach so "Nullteiler" heißt.

Danke!

Sei f(t) eine Funktion mit
t ist Zeit
f(t) ist km, m, Anzahl, l, …

Was bedeutet dann ein bestimmtes Integral von 0 bis b oder von a bis b im Sachzusammenhang?

Und wie kann man beweisen,dass eine Funktion stetig ist?

Hey, die Aufgabe lautet wie folgt:

Nun habe ich den Flächeninhalt ausgerechnet und kam auch zu der angegebenen Lösung jedoch bin ich mir unsicher ob meine Variante wirklich so richtig ist.

Das war mein Ansatz:

Doch wäre es so eigentlich nicht wirklich richtig:

(hier kommt man auch auf die angegebene Lösung)

Welcher Ansatz stimmt aber denn jetzt nun und wieso?

Danke jetzt schonmal

Hey ich habe 2 Fragen. Normalerweise kann ich das globalverhalten rationaler funktionen bestimmen aber von diesen 2 nicht.

1. Globalverhalten von 1/x².

Es ist ja eine Hyperbel. Wäre es dann ,,Für x gegen plus unendlich gilt: f(x)->0 und das selbe mit minus unendlich?

2. Globalverhalten von 5x+ Wurzel x

Es ist eine proportionale Funktion aus dem Ursprung. Sie geht für x gegen Plus unendlich nach +○○ aber für x gegen - unendlich?

Hallo liebe Community,

ich habe folgende Aufgabenstellung( siehe Bild) . Bei der ersten Aufgabe soll überprüft werden, ob eine sigma Algebra vorliegt.
Bei der zweiten Aufgabe hingegen ob X eine Zufallsgröße über dem Wahrscheinlichkeitsraum ist. Mit der ersten Aufgabe komme ich noch zurecht, aber mit der zweiten nicht wirklich. Ich habe die Begriffe nicht wirklich verstanden und weiß daher nicht wie ich vorzugehen habe. Könnt ihr mir weiterhelfen?

Wie berechne ich das Integral? Reihenentwicklung eventuell?

Wir wissen alle, dass die 0 unendlich oft in die 1 passt, und wer was anderes behauotet, hat keine Ahnung, aber wie oft passt sie in die 0, also in sich selbst?

0-mal, 1-mal oder unendlich?

Die Herleitung der Formel (über eine DGL) mit nur einem Vorwiderstand, ist mir bekannt. Die Zeitkonstante tao ändert sich jedoch bei parallelem Widerstand zu (Rv||Rp)*C. Um das Nachvollziehen wäre eine Herleitung sehr hilfreich. Auch ein Link zu der entsprechenden Herleitung wäre ausreichend, da ich nichts finden konnte.

Was ist der Unterschied von

K(t) und K(n) ?

Beide beschreiben doch das Kapital nach so und so viel Jahren.. warum gibt es unterschiedliche Bezeichnungen dafür?

Wie kommt man da auf die Lösung?

Es gilt zu beweisen, dass 3^n-3 (n>=1) immer durch 6 teilbar ist. Im Internet sah ich mehrere Lösungsvorschläge, keiner der aussah wie meiner. Ich ging so vor:

Induktionsbeginn: 3^1-3=0/6=0 -> passt

Induktionsbehauptung: 6 teilt 3^n-3

Induktionsschritt: 3^(n+1)-3=3*3^n-3 -> man kann 3 ausklammern =3(3^n-1) und sieht nun, dass 3^n-1 immer gerade ist, weil 3^n ungerade ist und eine ungerade Zahl -1 wieder gerade. Damit hat man mit 3^(n+1)-3 eine sowohl durch 2, als auch 3 teilbare Zahl, die logischerweise auch durch 6 teilbar ist.

Gibt es einen mathematischen Beweis dafür, dass 1 Plus 1 vielleicht nicht zwei ist?

Hallo wie kann ich erkennen an einer Funktion ob sie gerade oder ungerade ist?

Welche spezielle Mathematische Funktion beindruckt/gefällt euch am meisten? Freue mich auf Antworten :)

Wie kommt man da auf die Lösung? Ich bin echt überfordert haha

sin(x) = 1/2 / arcsin rechts und links anwenden

arcsin * sin(x) = arcsin(1/2) Warum zieht man jetzt hier die 1/2 auf der rechten Seite der Gleichung in den arcsin rein, d. h. in die Klammer und nicht:

arcsin * sin(x) = arcsin * 1/2 ???

Gegeben ich habe folgende Informationen, wie kann ich daraus am einfachsten die Kovarianzmatrix berechnen?

Mein Ansatz ist der folgende

Cor(X,Y) = Cov(X,Y) / (σx * σy)

Das kann ich nach der Kovarianz umstellen. Aber wie funktioniert das mit ganzen Matrizen?

Hat jemand eine Idee wie ich die a lösen könnte also wie ich vorgehen muss? Wäre um einen Rat dankbar

Hallo ich habe eine Aufgabe gemacht jedoch verstehe ich nicht wie ich die d) und e) machen kann denn es ist ja zb.: x/a=m/y und auf dem Bild ist a gegeben und x nicht und bei m/y ist m gegeben und y nicht und deshalb wollte ich fragen wie ich es da dann herausfinden kann