Schweres Integral?
Wie kommt man da auf die Lösung? Ich bin echt überfordert haha
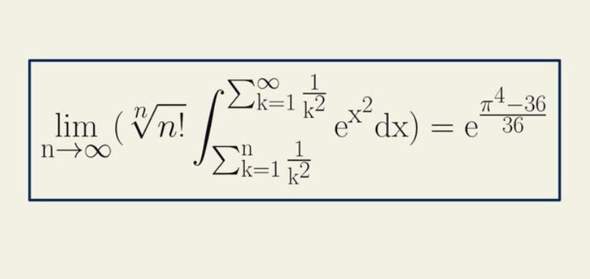
2 Antworten
Ich schaffe es nicht ganz das Integral zu lösen, da das wirklich schwer ist.
Ich würde deswegen nur meinen Ansatz teilen, in der Hoffnung, dass der vielleicht jemanden weiterhilft oder dass da jemand einfach weitermachen kann, und ich würde noch eine Alternative nennen.
Integral (was ich geschafft habe)Zuerst würde ich eine Stammfunktion bestimmen via Reihenentwiklung:
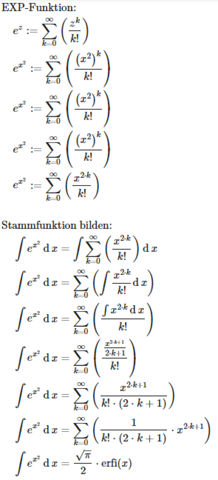
\begin{align*}
&\text{EXP-Funktion:}\\
&\quad e^{z} := \sum\limits_{k = 0}^{\infty} \left( \frac{z^{k}}{k!} \right)\\
&\quad e^{x^{2}} := \sum\limits_{k = 0}^{\infty} \left( \frac{\left( x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{x^{2}} := \sum\limits_{k = 0}^{\infty} \left( \frac{\left( x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{x^{2}} := \sum\limits_{k = 0}^{\infty} \left( \frac{\left( x^{2} \right)^{k}}{k!} \right)\\
&\quad e^{x^{2}} := \sum\limits_{k = 0}^{\infty} \left( \frac{x^{2 \cdot k}}{k!} \right)\\
\\
&\text{Stammfunktion bilden:}\\
&\quad \int e^{x^{2}} \operatorname{d}x = \int \sum\limits_{k = 0}^{\infty} \left( \frac{x^{2 \cdot k}}{k!} \right) \operatorname{d}x\\
&\quad \int e^{x^{2}} \operatorname{d}x = \sum\limits_{k = 0}^{\infty} \left( \int \frac{x^{2 \cdot k}}{k!} \operatorname{d}x \right)\\
&\quad \int e^{x^{2}} \operatorname{d}x = \sum\limits_{k = 0}^{\infty} \left( \frac{\int x^{2 \cdot k} \operatorname{d}x}{k!} \right)\\
&\quad \int e^{x^{2}} \operatorname{d}x = \sum\limits_{k = 0}^{\infty} \left( \frac{\frac{x^{2 \cdot k + 1}}{2 \cdot k + 1}}{k!} \right)\\
&\quad \int e^{x^{2}} \operatorname{d}x = \sum\limits_{k = 0}^{\infty} \left( \frac{x^{2 \cdot k + 1}}{k! \cdot \left( 2 \cdot k + 1 \right)} \right)\\
&\quad \int e^{x^{2}} \operatorname{d}x = \sum\limits_{k = 0}^{\infty} \left( \frac{1}{k! \cdot \left( 2 \cdot k + 1 \right)} \cdot x^{2 \cdot k + 1} \right)\\
&\quad \int e^{x^{2}} \operatorname{d}x = \frac{\sqrt{\pi}}{2} \cdot \operatorname{erfi}\left( x \right)\\
\end{align*}
wobei Erfi die imaginäre Fehlerfunktion von Euler ist.
Dann würde ich die obere Integralgrenze ausrechnen:
Die obere Integralgrenze ist einfach nur die Reihenentwicklung der Riemannschen Zeta Funktion von 2, welche Euler bereits gelöst hat. Diese Lösung ist als die Lösung des Basel-Problems bekannt:
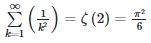
\sum\limits_{k = 1}^{\infty} \left( \frac{1}{k^{2}} \right) = \zeta\left( 2 \right) = \frac{\pi^{2}}{6}
Dann würde ich alles einmal einsetzen und gucken was dann dasteht, da das recht schwer aussieht:
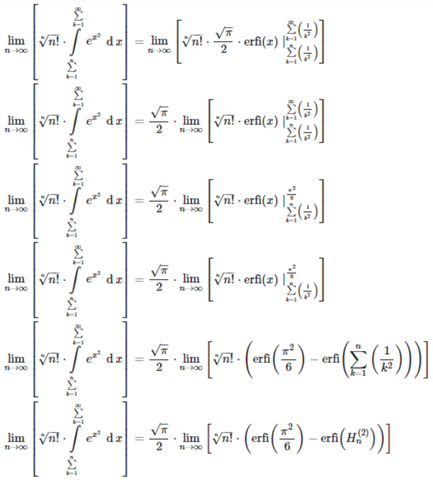
\begin{align*}
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \frac{\sqrt{\pi}}{2} \cdot \operatorname{erfi}\left( x \right) \mid_{\sum\limits_{k = 1}^{n} \left( \frac{1}{k^{2}} \right)}^{\sum\limits_{k = 1}^{\infty} \left( \frac{1}{k^{2}} \right)} \right]\\
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \frac{\sqrt{\pi}}{2} \cdot \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \operatorname{erfi}\left( x \right) \mid_{\sum\limits_{k = 1}^{n} \left( \frac{1}{k^{2}} \right)}^{\sum\limits_{k = 1}^{\infty} \left( \frac{1}{k^{2}} \right)} \right]\\
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \frac{\sqrt{\pi}}{2} \cdot \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \operatorname{erfi}\left( x \right) \mid_{\sum\limits_{k = 1}^{n} \left( \frac{1}{k^{2}} \right)}^{\frac{\pi^{2}}{6}} \right]\\
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \frac{\sqrt{\pi}}{2} \cdot \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \operatorname{erfi}\left( x \right) \mid_{\sum\limits_{k = 1}^{n} \left( \frac{1}{k^{2}} \right)}^{\frac{\pi^{2}}{6}} \right]\\
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \frac{\sqrt{\pi}}{2} \cdot \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \left( \operatorname{erfi}\left( \frac{\pi^{2}}{6} \right) - \operatorname{erfi}\left( \sum\limits_{k = 1}^{n} \left( \frac{1}{k^{2}} \right) \right) \right) \right]\\
\lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \int\limits_{\sum\limits_{k = 1}^{n}}^{\sum\limits_{k = 1}^{\infty}} e^{x^{2}}\, \operatorname{d}x \right] &= \frac{\sqrt{\pi}}{2} \cdot \lim\limits_{n \to \infty}\left[ \sqrt[n]{n!} \cdot \left( \operatorname{erfi}\left( \frac{\pi^{2}}{6} \right) - \operatorname{erfi}\left( H_{n}^{\left( 2 \right)} \right) \right) \right]\\
\end{align*}
wobei das H_{n}^{(r)} für die verallgemeinerten harmonischen Zahlen stehen. Alternativ wird auch H_{n,\, r} genutzt, aber online Rechner werden wohl ehr was mit ersteren Anfangen können.
Wolfram|Alpha sagt auf die Eingabe sinngemäß "Kein Plan!", was bedeutet dass es noch schwerer wird als gedacht, da ich definitiv nicht besser bin als Wolfram|Alpha im Berechnen von unendlichen Summen und Grenzwerten. Es findet aber auch auch die "schöne" dazugehörige Reihentwicklung, wo wir auch schon das exp(pi^{4}) sehen und die 36:

Da Sqrt[n]{n!} gegen unendlich geht wenn n gegen 0 geht, aber das gesamte Konstrukt nicht 0 ist, würde ich die Verwendung der Regel von l`hopital probieren, doch da die Fakultät nur für natürliche Zahlen und die 0 definiert ist, also eine reellwertige Ableitung davon nicht definiert ist, würde das wohl versagen. Sagen wir, dass die Fakultät hier durch die Gammafunktion auch für reelle n ersetzt werden kann, dann könnten wir es mit der Polygammafunktion ableiten, wo mir Wolfram|Alpha liebevoll mitteilt "Ich habe keine Ahnung, da ich nicht einmal die Eingabe verstehe.".
So und das ist der Punkt an den ich aufgebe, da ich komplexe Grenzwerte wohl kaum selbst berechnen kann und Wolfram|Alpha jetzt schon aufgegeben hat, also "die letzte Hoffnung" tot ist.
Letzte Alternative:Das ist wohl eine gute Frage für "https://math.stackexchange.com/questions/ask", da dort die Frage einer breiteren Menge guter Mathematiker präsentiert wird von denen wahrscheinlich jemand helfen könnte.
Das Forum hat wesentlich höhere Qualitäts-Standards, weswegen sich dort auch in der Regel qualitativ hochwertigere Antworten rumschleichen und es hat einen wunderbaren LaTeX-Editor "MathJax" (den ich auch immer für meine LaTeX Formeln nutze).
Die Zusammenarbeit der anderen würde zudem wahrscheinlich auch zu vielen diversen Ansätzen führen.
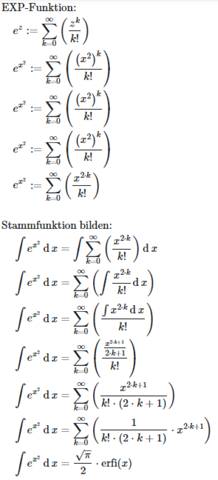
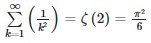
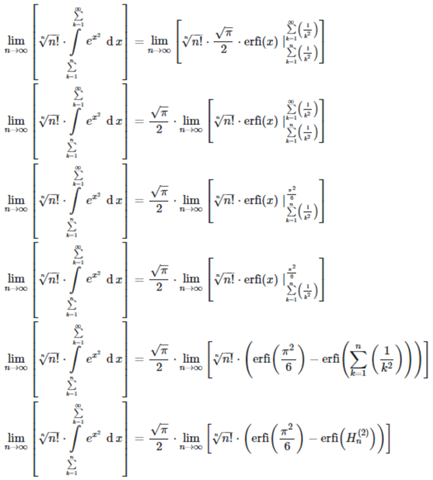

Ich bin dort angemeldet, jedoch mit meinen echten Daten, mit welchen man meine Person in rl ausfindig machen könnte und ich fände es nicht als zu gut, würde man alles was ich in Internet mache auf mich als Person zurückführen können.
Alles gut, dann mache ich das mal in den nächsten Tagen. Danke!
Der erste Faktor (n!)^(1/n) kann mit Hilfe der Stirling-Formel approximiert werden,
(2 Pi n)^(1/2n) n/e
Das Integral kann mit dem Mittelwertsatz als Intervallänge mal Funktionswert an einem Zwischenwert geschrieben werden,
Summe( k > n; 1/k^2 ) exp( xi^2 )
Die Summe kann durch ein Integral über 1/x² ab 1/n approximiert werden, macht 1/n plus irgendein Rest. xi schreibt man als Pi^2 /6 + O(1/n).
Den Grenzwert für n gegen unendlich sieht man jetzt wie folgt ein:
(2 Pi n)^(1/2n) geht gegen 1
n/e Summe( k > n; 1/k^2 ) gehen gegen 1/e
exp( xi^2 )geht gegen Pi^4 / 36
Das zusammen gibt den Grenzwert.
Was bleibt ist die Sache mit den Fehlerabschätzungen, was noch sauber aufzuarbeiten ist, viel Vergnügen.
Bist du dort angemeldet? Wenn ja, könntest du dort die Frage stellen? Will mich nicht extra anmelden