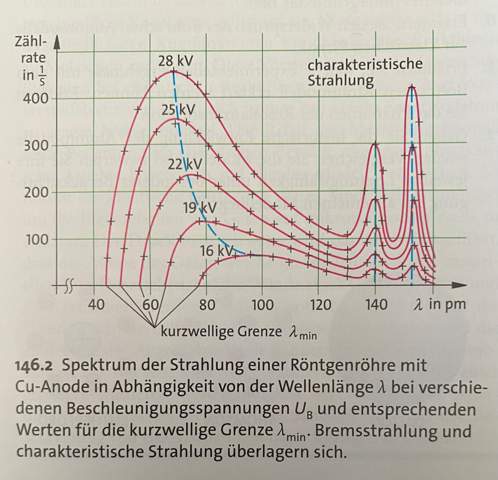
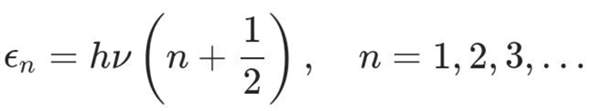2. In Abbildung 146.2 sind Röntgenspektren für verschiedene Beschleunigungsspannungen dargestellt. Ermit-feln Sie jeweils die Grenzwellenlänge. Stellen Sie di?
- In Abbildung 146.2 sind Röntgenspektren für verschiedene Beschleunigungsspannungen dargestellt. Ermit-feln Sie jeweils die Grenzwellenlänge. Stellen Sie die kinetische Energie der beschleunigten Elektronen in Abhängigkeit von der Grenzfrequenz dar. Ermitteln Sie aus diesem Diagramm die Plancksche Konstante.
- In Abb. 146.2 sind zwei Spektrallinien zu erkennen. Bestimmen Sie jeweils die Wellenlänge und ordnen Sie diese der K~- bzw. der K -Strahlung zu. Bestimmen Sie mithilfe obiger Formel die zugehörige Ordnungszahl des Anodenmaterials.
Hey, ich bräuchte Hilfe bei der Lösung beider Aufgaben. Am besten wäre es, wenn ihr mir vielleicht Formeln nennen könntet die weiterhelfen.