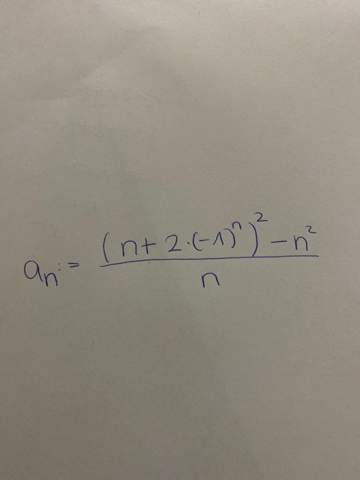Limes – die besten Beiträge

Ich verstehe eine Aufgabe nicht wirklich bzw. weiß ich nicht wie ich es beantworten soll.

Die Aufgabe:

Zeigen Sie, dass die harmonische Reihe trotz

 nicht konvergiert.

Also das was ich sagen würde ist, das man und der harmonischen Reihe wir die 1 + 1/2 + 1/3 + 1/4 + ... etc addieren . Die Kehrwerte (1/n) werden immer kleiner, aber sie werden nie so klein, dass die Summe der Reihe aufhört zu wachsen (Sie wird immer größer und größer). Also sie divergiert, weil sie keine feste obere Grenze hat und unendlich wird.

Reicht das so oder wie soll ich es erklären?

Wie berechnet man diese Limetes?

Bin vor allem wegen Alpha verwirrt.

Hallo!

Ich habe versucht, etwas zu beweisen, und ich habe es vielleicht geschafft. Ich glaube aber nicht, da sich die Dinge in der Unendlichkeit anders verhalten sollten. Aber man weiß ja nie. Der Beweis ist für die Irrationalität von Gamma(Euler-Mascheroni-Konstante):

γ = lim(n->∞ H(n)-ln(n))

ln(n) mit n ∈ N, n ≠ 1 ist immer irrational. Beweis:

Wählen wir ein x ∈ N, x ≠ 1

f^-1(e^x) = ln(x)

e ist transzendent, also ist e^x nie eine natürliche Zahl. Oder: ln(x) ∉ N

Und H(n) divergiert, also konvergiert es nicht gegen eine Irrationale Zahl. Und da wir nur rationale Zahlen addieren, bleibt H(n) immer rational.

Und irrational minus rational ist irrational.

Und da wir bei

γ = lim(n->∞ H(n)-ln(n))

eine irrationale Zahl minus eine rationale rechnen, müsste es - denke ich - immer irrational sein.

Ich glaube aber, dass sich das bei der Unendlichkeit anders verhält und der Beweis deshalb falsch ist. Denn Leonhard Euler wäre bestimmt auf so etwas gekommen.

Danke!

Hallo!

Ich würde gerne wissen, wie man so eine Gleichung umformt:

lim n->0 (x/(n-1)) = 1

Das war jetzt natürlich nur ein Beispiel. Da ist -1 ganz klar die Lösung.

Aber wie kann man solche Gleichungen umformen? Ich habe mal folgendes gesehen:

Man nimmt die Gleichung, lässt den Limes weg und schreibt ihn am Ende wieder auf die andere Seite. Geht das immer?

Ich bin verwirrt, wo ist der Unterschied ob man eine Ableitung mit der Limes Formel oder mit den Ableitungsregeln ausrechnet, es kommt doch aufs gleiche hinaus?

Ist es nur eine andere Möglichkeit auf das gleiche Ergebnis zu kommen? Was davon ist einfacher?

Ich bin auf das Problem gestoßen, als ich jemanden beantworten wollte, was das ergibt wenn wir z als komplexe Zahl betrachten:



Das war kein Problem, doch beim lösen mit Rechenweg musste ich das Limit aus den Argument von z ziehen bzw. arg(z) so verallgemeinert habe, dass es sich am Ende aufgelöst hatte, doch das funktioniert nur für z -> 0.

Daher hatte ich mich gefragt, was denn so das Limit für ein paar Argumente ist, weshalb ich Wolfram|Alpha gefragt habe und Wolfram|Alpha kann das irgendwie berechnen. (z.B. lim_{x -> 0^-} arg(x) = pi und lim_{x -> 0^+} arg(x) = 0)

Da frage ich mich einfach, wie Wolfram|Alpha das berechnet?

Mir würde nur einfallen, dass man z in Realteil x und Imaginärteil y unterteilt, dann die verallgemeinerte arctan2-Funktion nutzt und dann daraus das Limit zieht:

Doch ich glaube nicht, dass Wolfram|Alpha das macht / kann.

Hallo, wie muss man bei der Grenzwertberechnung mit Limes vorgehen wenn der größte exponent des Zählers größer ist als der beim Nenner?

Ist das Ergebnis richtig? Also habe ich die h's richtig weggekürzt?

Hi, hier einmal die Aufgabe:

Also die Fibonacci Reihe konvergiert ja gegen den Goldenen Schnitt. Ich verstehe nur nicht wie ich die Aufgabe hier löse, obwohl sich eigentlich so simpel ist…:(

Hoffe jemand kann mir kurz helfen, steh grad aufm Schlauch.

Gruß

hallo

Weiß einer wie ich hier auf den Limes inferior und superior komme?

ich bedanke mich im Voraus

Laut Lösung ist der Limes inf=-4 und der Limes sup=4

Für lim x --> 0.

Ich habe als Ergebnis 1/e. Nun ist das im Bereich von x = 0 der Grenzwert, wenn ich das richtig verstehe... Aber es könnte ja auch sein, dass der Bereich x < 0 nicht definiert wäre. Also muss ich doch immer links- und rechtsseitigen GW bestimmen? Wenn ja, wie gehe ich da vor... Ich blicke da noch nicht ganz durch.. :(

Derzeit besprechen wir in der Schule (11.Klasse) das Verhalten im unendlichen bei gebrochen rationalen Funktionen. Nun sind wir beim Themengebiet der waagrechten Asymptoten, beim Fall Zählergrad=Nennergrad.

Nun ist mir aber eine Frage aufgekommen, bei dem Blatt dass ich unten hinzugefügt habe verstehe ich nicht wieso dort 3- rauskommt und nicht 3+, da ja eigentlich nur Positive Werte vorhanden sind und somit etwas positives rauskommen müsste.(ich hoffe man versteht meine Problematik)Vielen Dank schonmal im Vorraus!

Guten Tag,

Ich habe mehrmals versucht, 2x^2 -x mit dem Limes abzuleiten, habe aber immer nur 4x rausbekommen, obwohl das Ergebnis 4x-1 ist. Kann mir jemand den Rechenweg zeigen?

Danke für Antworten.

War gestern E Scooter fahren und hab ein Abo abgeschlossen 5,99€ monatlich , bin über 30 min gefahren und die haben mir nur 3€ Gebühren abgezahlt, obwohl da 22€ stand nach der Fahrt? Warum wurden mir dann nur 3€ abgezogen?

Hallo, Ich brauche hilfe ich besitze kein Paypal und meine Eltern erlauben es mir nicht ich will aber Lime Scooter Fahren kann mann da iwie nur mit dem Guthaben zahlen (hab 5€) ODer irgendwie leere paypal accounts wo verifiziert sind kriegen bitte um schnelle antwort btw. bin 13 werde am 17. 14

Danke im Voraus :=)

Hallo,

Ich habe wie fast alle momentan im Moment Homeschooling. Im Fach Geschichte haben wir gerade das große Thema "Das römische Reich". Wir bekommen in Geschichte meistens Arbeitsblätter. Diese Woche auch wieder. Auf dem Foto sehr ihr die "Aufgabenstellung". Leider ist mein Schulbuch nicht sehr toll und im Internet bin ich leider auch nicht schlau geworden. In meinem Buch steht eine halbe Seite Thema "Limes" aber nichts beschriftet. Noch ganz wichtig: Ist Limes überhaupt richtig? Ich denke schon, denn das sieht fast so aus wie der Limes auf dem Buch. Ich freue mich sehr über nette Antworten.

Liebe Grüße

Kann mir jemand angeben, ob die Funktion f(x)= 0,5x^2-3 den Grenzwert gegen unendlich oder minus unendlich hat?

Bzw. wie kann ich das ohne es zu zeichnen bestimmen?

Wie lange kann der offen sein und muss er nach Öffnung gekühlt werden?

Ich bedanke mich im Voraus !

Hallo zusammen,

Ich möchte unbedingt mit meinen Freunden mal E-Scooter fahren. Mein großer Cousin hat sich mal eine Prepaid Mastercard gekauft und ist damit gefahren. Wie kann ich mir mit 14 eine Prepaid Kreditkarte kaufen? Am besten mit Bargeld.

danke!