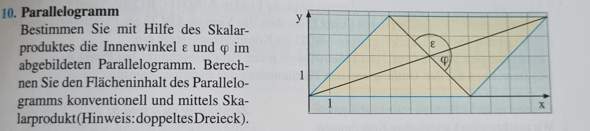
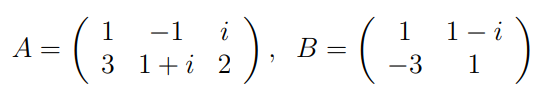Hallo, wer kann mir bei dieser Aufgabe helfen. Leider habe ich wenig Plan davon......vielleicht hat sie auch jemand schon einmal gerechnet...
Auf dem Marktplatz im Zentrum einer Stadt steht ein quadratische Pyramide mit 6m Seitenlänge und 7m Höhe. Anlässlich des Stadtjubiläums soll auf einer Seitenfläche eine quadratische Gedenktafel angebracht werden, die einer Seitenlänge von 1m hat.
a) Wie steil sind die Seitenflächen der Pyramide, unter welchem Winkel stoßen benachbarte Seitenflächen zusammen?
b) Es gibt Überlegungen, ob man zur Befestigung der Gedenktafel mit einem Bohrloch auskommen kann, wenn man senkrecht zur Seitenfläche so bohrt, dass der Bohrrichtung auf dem Mittelpunkt der der gegenüberliegenden Grundkante zielt.. Wählen sie einer der vier Seitenflächen aus und bestimmen Sie auf ihr die Lage des geplanten Bohrlochs. Beschreiben sie die Lage des Bohrlochs auf der Seitenfläche unabhängig von der gewählten Seitenfläche möglichst genau.
Vielen lieben Dank im Voraus