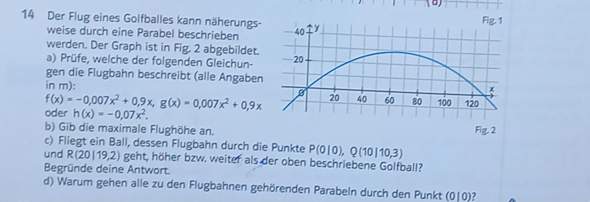
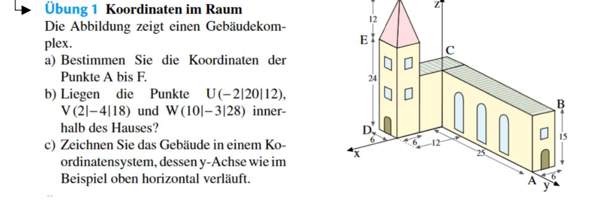
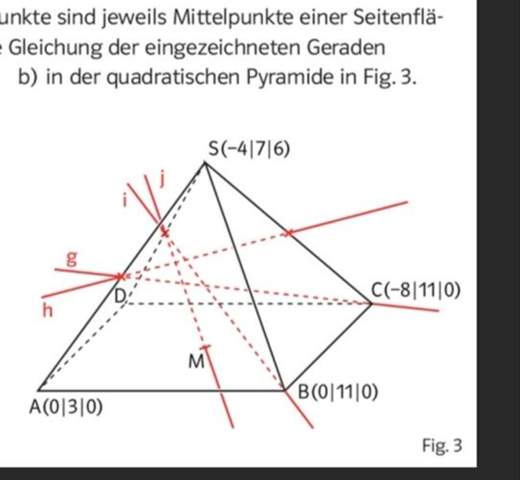
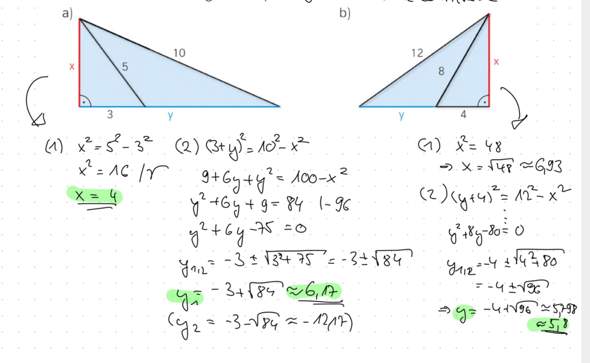
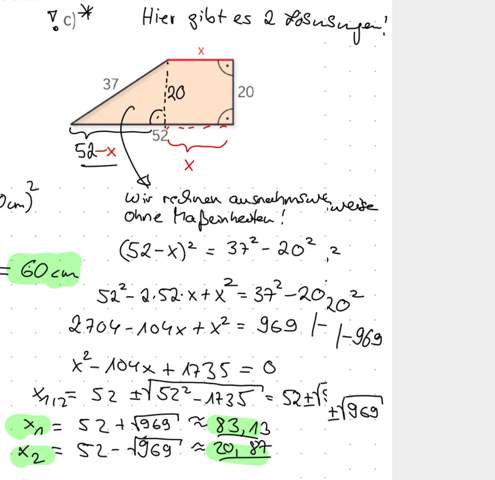
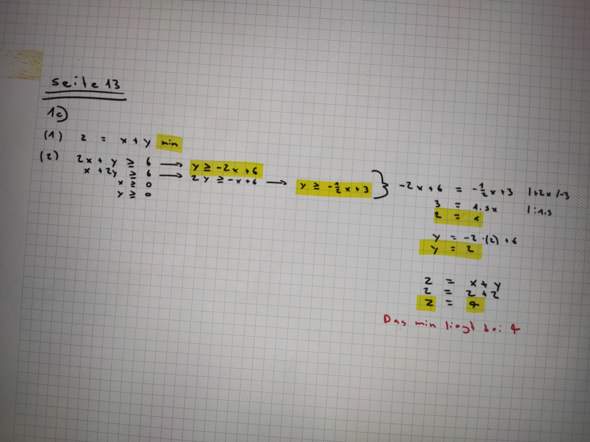
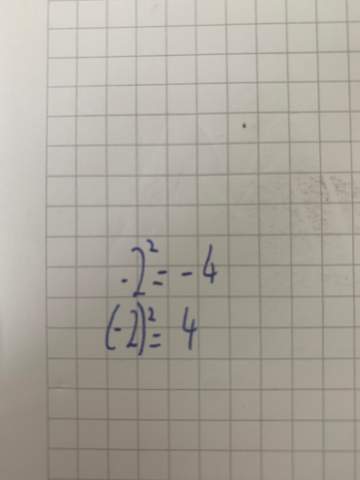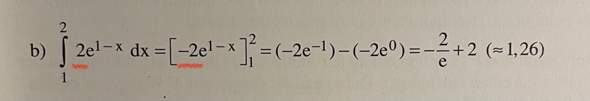Warum existiert kein globales Minimum im Intervall?
=> Das lokale Maximum für f(-2/3) ist auch das globale Maximum. Nachvollziehbar!
a) Warum existiert in diesem Fall aber kein (gloables) Minimum?
Wenn ich mich an den linken Randpunkt des Intervalls ]-1, -1/2] annähre. D. h.
f(-1 (+)) etwas größer als -1 z. B. -0,99, dann kommt doch - unendlich heraus.
b) => Ist dies Aufgrund des Intervalls ]-1,...] ? Da -1 ausgeschlossen ist?
Was wäre, wenn das Intervall einer beliebigen Funktion [-2,+2] ist. Und
c) f(-2) gegen -unendlich geht Wäre das dann ein globales Minimum? Oder wenn f(2) gegen + unendlich geht => globales Maximum. Hier sind ja die Randpunkte im Intervall eingeschlossen.