Stochastik kugeln?
Wie löse ich diese aufgabe?
Ich habe fur rot 66,6%
Für schwarz 19%
6 Antworten
Dein Ergebnis kann nicht stimmen , da beide P zusammen 100% ergeben müssen
Ich "klau" mir mal Hamburger02 seinen Baum
In den drei Pfaden steckt
zweimal rot
Davon ist einer mit Schw und zwei mit Rot
Daher 1/3 und 2/3
Ich verstehe es nicht. Für rot hab ich 2/3. Und für schwarz wäre es doch der Pfad 5/7*4/6*1/5, denn nur so hat man dass 2 rote und am Ende eine schwarze
Wenn von drei Kugeln genau 2 Rot sind und genau 1 Schwarz ist, dann gibt es nur die drei möglichen Abfolgen S R R , R S R und R R S. Nur bei einer diese drei Abfolgen ist Schwarz an dritter Position.
Wahrscheinlichkeit "2 von 3 rot": Es gibt 3 Pfade, alle mit gleicher Wahrscheinlichkeit:
r-r-s: 5/7 * 4/6 * 2/5
r-s-r: 5/7 * 2/6 * 4/5
s-r-r: 2/7 * 5/6 * 4/5
Dritte schwarz ist einer der drei Pfade, die bedingte Wahrscheinlichkeit ist also 1/3. Dritte rot ist damit 2/3.
Hallo,
mit Deinem Ergebnis für Rot bin ich einverstanden.
Bei Schwarz sehe ich das anders:
Es gibt nur drei Möglichkeiten, daß bei drei Ziehungen ohne Zurücklegen zweimal Rot dabei ist:
RRS, RSR, SRR.
Nur bei einer der drei ist Schwarz hinten.
Da alle drei Möglichkeiten mit der gleichen Wahrscheinlichkeit (4/21) auftauchen, teilst Du 4/21 durch 12/21; das ergibt 1/3 oder 33,33...%.
Herzliche Grüße,
Willy
Ja. Rot am Ende unter der Bedingung, daß zweimal Rot dabei ist: 2/3.
Schwarz am Ende unter der gleichen Bedingung: 1/3.
Ich verstehe es nicht. Für rot hab ich 2/3. Und für schwarz wäre es doch der Pfad 5/7*4/6*1/5, denn nur so hat man dass 2 rote und am Ende eine schwarze
Hier geht es um eine bedingte Wahrscheinlichkeit. Die Bedingung, daß zwei von drei Kugeln gezogen wurden, ist vorausgesetzt. Es gibt drei Kombinationen mit zwei roten und einer schwarzen Kugeln, die alle mit der gleichen Wahrscheinlichkeit auftreten. Nur bei einer von ihnen ist Schwarz hinten. Daher ein Drittel.
So sieht das Baumdiagramm aus:
Da suchen wir nun die Pfede raus, die am Ende eine rote Kugel haben und davor nur eine weitere rote Kugel haben. Das ist bei den Pfaden 4 und 6 der Fall.
Daher:
P = (2/7 * 5/6 * 4/5) + (5/7 * 2/6 * 5/5)
= 40/210 + 50/210 = 90/210 = 9/21 = 3/7 = 42,9 %
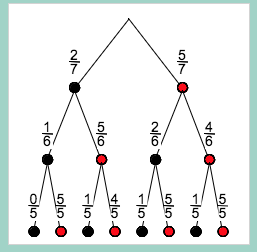
zwei von drei gezogenen Kugeln sollen rot sein , so lese ich die Aufgabe . Daher drei Pfade 4 , 6 und 8
Bei 8 sind aber drei und nicht zwei von drei Kugeln rot. Bei 8 hätte im Text ein "mindestens" erscheinen müssen.
Ja, aber das ist nicht, dass schwarz AM ENDE gezogen wird!!! Die dritte Kugel soll schwarz bzw rot sein