Kann mir einer bitte diesen Eintrag aus einem Mathe Buch erklären?
f(x) = x^3-2x^2 = x^2 (x - 2)
x1 = 0 (doppelte Nullstelle)
X2=2
Bemerkung: Da das konstante Glied im Funktionsterm fehlt, kann die Nullstelle X =0 durch Faktorisieren ermittelt werden.
Ich möchte wissen, warum dort doppelte Nullstelle steht und von welchem konstantem Glied da die rede ist.
und berechnet man Nullstellen einer Funktion 3 grades oder höher immer durch faktorisieren
3 Antworten
Normalerweise sieht so eine Funktion ungefähr so aus: ax³ + bx² + cx + d. In Deinem Fall sind aber die hinteren beiden Koeffizienten c=d=0 (dabei heißt d das konstante Glied, und c ist der Koeffizient des linearen Gliedes), und deshalb kannst Du x herausheben und bekommst x³−2x² = x² (x−2) und bekommst daraus sofort die beiden Nullstellen x₁=x₂=0 und x₃=2.

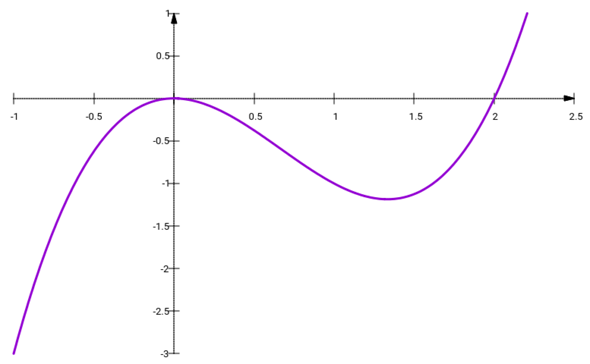
Im Graphen siehst Du die Nullstelle bei x=2, und die doppelte Nullstelle bei x=0. Daß sie doppelt ist, erkennst Du daran, daß sie gleichzeitig eine Nullstelle und ein Extremum (in diesem Fall Maximum) ist (und wenn Du ein bißchen über die Produktregel nachdenkst, siehst Du ganz klar, warum ein Faktor (x−a)² in einer Funktion grantiert, daß sowohl die Funktion als auch ihre erste Ableitung bei x=a Null ist)
Das konstante Glied ist die Zahl ganz am Ende. Aber f(x) hat ja gar keine Zahl, es endet mit 2x^2. Richtigerweise ist das konstante Glied hier Null, aber die schreibt man nicht hin.
f(x) = 0 liefert x^2=0 oder (x-2)=0
Und x^2=0 liefert x=0 oder x=0
Also ist x=0 eine doppelte Nullstelle.
x^3-2x^2=0
x^2*(x-2)=0
Weil du x^2 ausklammern konntest gilt x_1=0 und x_2=0
Und mit x-2=0 ergibt sich x_3=2
Doppelte Nullstellen sind zwei Nullstellen die denselben Wert haben.
Wenn du x^2 ausklammern kannst, dann ja. Dann sind die Nullstellen zwei mal an der Stelle x=0
Gibt es auch an anderen Stellen, zum Beispiel:
f(x) = 2 * x * (x - 1) * (x - 1) = 2 * x ^ 3 - 4 * x ^ 2 + 2 * x
Da liegt die doppelte Nullstelle bei x=1
Achso, das ist eine doppelte Nullstelle weil das x quadriert ist? Dankeschön. Am Graphen erkennt man das aber nicht oder? also dass es an der stelle 2 Nullstelle gibt