Wie kann man Nullstellen erraten, wenn die Nullstellen ungerade sind?

Bei Polynomdivision 

Comments

[Franz1957]

Meinst Du ungerade Zahlen? Oder meinst Du nichtganze Zahlen ("Kommazahlen")?

[Monstrum11111]

Kommazahlen.

Answer 1

[DerRoll]

Generell gilt dass wenn es eine ganzzahlige Nullstelle gibt sie sich im Absolutglied, also dem Teilterm ohne x, als Faktor versteckt. Ist KEIN Absolutglied in der Funktion, so klammert man so viele x aus wie erforderlich bis man eine Funktion mit Absolutglied hat. In diesem Fall ist bereits eine Nullstelle, nämlich die 0 in der Vielfachheit wieviele x man ausgeklammert hat, bekannt.

Comments

[Monstrum11111]

Bei manchen Gleichungen kann aber nicht ausklammern.

[DerRoll]

@Monstrum11111

Entweder du kannst ein x ausklammern oder du hast ein Absolutglied welches faktorisiert werden kann. Eines von beiden MUSS immer der Fall sein.

Answer 2

[mihisu]

Ok, du meinst eher nicht-ganze Zahlen (statt „ungerade“ Zahlen).

Da hilft dir vielleicht der sogenannte Satz über rationale Nullstellen. Damit kannst du zumindest alle rationalen Nullstellen eines Polynoms mit ganzzahligen Koeffizienten finden.

https://de.wikipedia.org/wiki/Satz_über_rationale_Nullstellen

Wenn du ein Polynom n-ten Grades

$f(x)=a_n\cdot x^n +a_{n-1}\cdot x^{n-1}+\ldots + a_1\cdot x+a_0$

mit ganzzahligen Koeffizienten aₙ, ..., a₀ ∈ ℤ betrachtest, so kann jede rationale Nullstelle des Polynoms als p/q dargestellt werden, wobei p ein Teiler von a₀ ist und q ein Teiler von aₙ ist.

Beispiel:

$f(x)=5\, x^3+3\, x^2+13\,x-6$

• Die Teiler von -6 sind -6, -3, -2, -1, 1, 2, 3, 6.
• Die Teiler von 5 sind -5, -1, 1, 5.

Als Kandidaten für die rationalen Nullstellen kommen demnach in Frage...

$\pm\frac{1}{1},\ \pm\frac{2}{1},\ \pm\frac{3}{1},\ \pm\frac{6}{1},\ \pm\frac{1}{5},\ \pm\frac{2}{5},\ \pm\frac{3}{5},\ \pm\frac{6}{5}$

Diese Nullstellen-Kandidaten kann man nun in die Polynomfunktion einsetzen, und schauen, ob man dort 0 als Funktionswert erhält. Tatsächlich erhält man bei diesem Beispiel f(2/5) = 0, sodass 2/5 eine Nullstelle der Polynomfunktion ist.

Einschränkungen:

• Man braucht ein Polynom mit ganzzahligen Koeffizienten. Bzw. wenn man rationale Koeffizienten hat, kann man zumindest durch passendes Ausklammern eines Faktors ein Polynom mit ganzzahligen Koeffizienten und den gleichen Nullstellen erhalten, mit dem man weiterarbeiten kann. Wenn man beispielsweise x³ + 3/5 x² + 13/5 x - 6/5 hat, kann man 1/5 ausklammern, um 1/5 (5 x³ + 3 x² + 13 x - 6) zu erhalten und damit das Polynom 5 x³ + 3 x² + 13 x - 6 mit den gleichen Nullstellen zu finden.
• Man findet so nur die rationalen Nullstellen. Wenn es keine rationalen Nullstellen gibt, findet man natürlich keine Nullstellen.

Answer 3

[Halbrecht]

unmöglich

hat eine Fkt wirklich nur Nullstellen mit Nachkommastellen , kann man es nicht schaffen
man kann sich durch Probieren an eine herantasten und hoffen , dass sie ein Bruch ist mit Nenner kleiner 10

bei dieser Fkt würde man nicht mal x0 = 9 finden

Answer 4

[Ougdo]

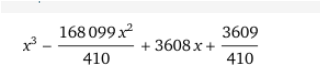
Man ratet mit den Teilern von der Konstante ohne x

Also sagen wir du hast ax^3+bx^2+cx+d

Dann schaust du was d für Teiler hat und versuchst die in einzusetzen. Klappt fast immer

Answer 5

[Roguerouge]

3 2 1 0 -1 -2 -3

probieren.

Comments

[Monstrum11111]

Ich meine Kommazahlen, AlSO wenn die Nullstellen 1,2562 oder so sind.

[Roguerouge]

@Monstrum11111

Ungerade Zahlen sind 1, 3, 5...

Was du meinst sind Nachkommazahlen oder auch reelle Zahlen.

[Monstrum11111]

@Roguerouge

Ja mein Gehirn hat gelaggt.