Wie löse ich diese Aufgabe?

ich hab ja gar keine seitenlänge gegeben

Answer 1

[merkurus]

Aufgabe 8
---
Wurzel(5,4² + 3²) = 6,177378
---
6,177378 * SIN(47,7) = 4,568981
---
x = 4,568981 * COS(35,4) = 3,724303
x beträgt 3,7243 cm

Answer 2

[RSL8a]

Gegeben:

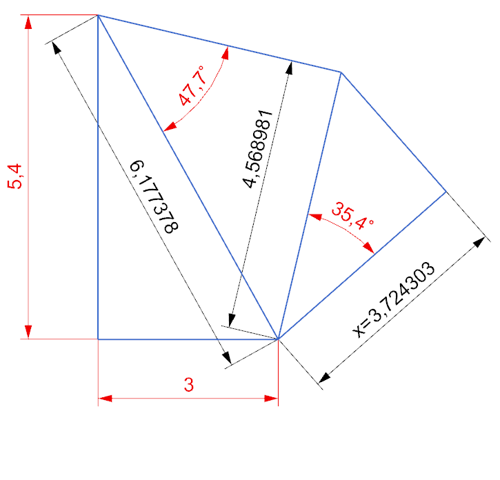
• Seitenlängen: a = 5,4 cm, b = 3,0 cm
• Winkel: γ = 96,9°

Lösung mit dem Kosinussatz:

Der Kosinussatz lautet:

x² = a² + b² - 2 mal a mal b mal cos(γ)

1. Werte einsetzen:

x² = 5,4² + 3,0² - 2 mal 5,4 mal 3,0 mal cos(96,9°)

x² = 29,16 + 9,00 - 32,4 mal cos(96,9°)

2. Kosinuswert berechnen:

cos(96,9°) ≈ -0,127

x² = 29,16 + 9,00 - 32,4 mal (-0,127)

x² = 38,16 + 4,12

x² = 42,28

3. Wurzel ziehen:

x = Wurzel von 42,28

x ≈ 6,5 cm

Antwort:

Die gesuchte Strecke x ist exakt Wurzel von 42,28 cm oder gerundet ca. 6,5 cm.

Answer 3

[Halbrecht]

erst Pyth im Dreieck mit 5.4 und 3.0

dann im DrEck mit 47.7 Sinus

dann im DrEck mit x Cosinus

Answer 4

[Wiesel]

Du hast drei rechtwinklige Dreiecks. Da denke ich zuerst an den SATZ DES PYTHAGORAS. und wenn ich irgendwo Winkel sehe, denke ich SINus, COSinus &TANgens

Versuche es mal damit 😁