Lineares Algebra Dreieck rechteckig?
wir sollen Aufgabe a und b machen, aber ich weiß nicht welche Schritte ich da befolgen soll

3 Antworten
Ich würde das so lösen:
a)
Winkel α
AB = B - A = (-4/3/2)
AC = C - A = (-1/7/2)
Mal schauen, ob die schon rechtwinklig sind:

nächster Versuch Winkel γ:
BC = C - B = (3/4/0)

letzter Versuch β:

q.e.d.
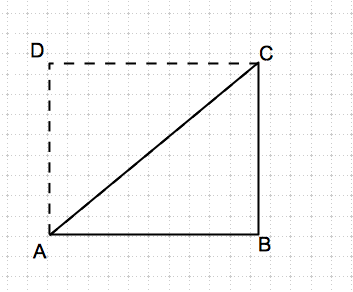
b) Hier hilft eine Skizze weiter:

D = A + BC = (8/6/2)



(a) Nachweis, dass das Dreieck ABC rechtwinklig ist:
Gegeben:
- A(5, 2, 2)
- B(1, 5, 4)
- C(4, 9, 4)
Berechne die Quadrate der Seitenlängen mit der Abstandsformel:
- AB² = (1-5)² + (5-2)² + (4-2)²
- = (-4)² + 3² + 2²
- = 16 + 9 + 4
- = 29
- BC² = (4-1)² + (9-5)² + (4-4)²
- = 3² + 4² + 0²
- = 9 + 16 + 0
- = 25
- AC² = (4-5)² + (9-2)² + (4-2)²
- = (-1)² + 7² + 2²
- = 1 + 49 + 4
- = 54
Da gilt: AB² + BC² = 29 + 25 = 54 = AC², folgt aus a² + b² = c², dass das Dreieck rechtwinklig ist (hier im Winkel an Punkt B).
(b) Bestimmung des vierten Punktes D, so dass ABCD ein Rechteck ist:
Der fehlende Eckpunkt D erhält man mit der Formel: D = A + C - B
Berechnung der Koordinaten: Dₓ = 5 + 4 - 1 = 8 Dᵧ = 2 + 9 - 5 = 6 D𝓏 = 2 + 4 - 4 = 2
Also lautet D = (8, 6, 2).
anstatt nachzufragen könnest du auch mal respekt mit danke sagen ? Oder haben dir deinen Eltern es verboten ?
Oder du könntest andere Leute ihre Angelegenheiten regeln lassen, oder als fremder Moralapostel zu intervenieren?
nee nee , das muss sein . Und fremder Leute Angelegenheiten gibt es in der Öffentlichkeit , die GF darstellt nicht
Sorry, dass es eine Aufzählung beim posten geworden ist. Bitte die Nummerierung ignorieren.
Für die a) würde ich alle Strecken ausrechnen und schauen ob man den Satz des Pytagoras anwenden kann. Für die b) musst du dir das Bildlich vorstellen: Du hast die Ecke mit dem einen rechten Winkel, nennen wir sie A. Von da aus geht es den Vektor AB in Richtung B und AC in Richtung C, um 90° Winkel eben. Jetzt musst du halt von dem Dritte zum vierten Eckpunktt den selben Vektoren anwenden. Also Vektor AB = Vektor CD.
Hängt aber eben ab davon, welche Ecke den 90° Winkel hat.
Muss es bei a nicht die Länge der Vektoren sein?