Gibt es eine solche funktion?
Gibt es eine Funktion f(x), die achsensymmetrisch zur y-Achse ist, aber an der Stelle x=0 nicht die Steigung 0 hat?
8 Antworten
Es gibt keine in x=0 differenzierbare Funktion, die zusätzlich achsensymmetrisch ist.
An der Stelle x = 0 ist die Ableitung 0, ist also keine Lösung.
Nur wenn die Steigung bei x=0 undefiniert ist.
Das ist nur bei in x = 0 nicht differenzierbaren Funktionen möglich, denn anderenfalls gilt wegen
auf Grund der Kettenregel
also an der Stelle x = 0
Für differenzierbare Funktionen kann es dies nicht geben, das eine Folgerung aus dem
https://de.wikipedia.org/wiki/Satz_von_Rolle
(lasse die obere und untere Intervallgrenze gleichzeitig und gleich schnell gegen 0 gehen).
Für nicht im ganzen Intervall differenzierbare Funktionen hat dir ein User bereits ein Gegenbeispiel gegeben.
Sicher. Z. B. f(x) = 1/x²

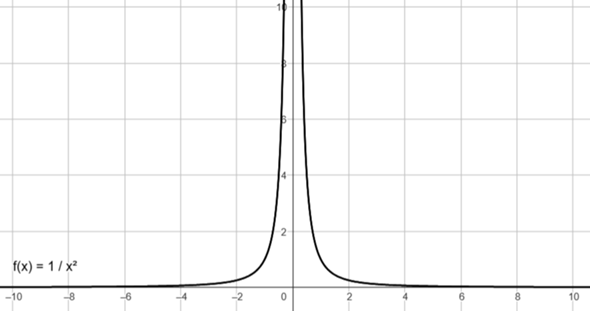
F(x)=x^2