2 Körper?
Wenn die ebene in grau den Quader schneidet, entstehen 2 Teil Körper.
Und vom diesen müsste ich das Volumen berechnen.
Ich würde zuerst das Volumen des Körpers
Hinter der ebene berechnen. Und für den 2. Körper dann das gesamte Volumen des Quaders - das Volumen des 1. Körpers rechnen
Allerdings verstehe ich nicht welcher Körper denn sich hinter der ebene befindet und wie ich da das volumen berechne...von der grundfläche ist es ein trapez, aber mit einer Spitze?

4 Antworten
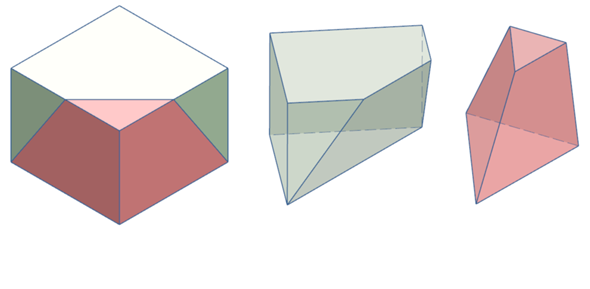
Schau dir mal folgendes Bild an.
Das rote ist ein Pyramidenstumpf. Läßt sich Volumen leicht berechnen.
V = (1/3) * h * (A1 + A2) + Wurzel(A1 * A2)
Das andere Volumen von grün bekommst du.
Quadervolumen ausrechnen minus Pyramidenvolumen.

Ich hab mal meinen Beitrag mit Formel ergänzt. Ich hab ja keine Maße. Also A1 und A2 sind ja jeweils Dreieckflächen. Fläche für Dreieck wirst du sicher kennen und die Maße kennst du ja. h ist die Höhe der Pyramide.
Aber diese Formel habe ich noch nicht gesehen....Ich kennen nur 1/3*G*h
Warum müsste ich für G die beiden Dreiecksflächen addieren?
1/3*G*h ist, wenn die Pyramide spitz ist. Ansonsten ergoogeln mit
Volumen Pyramidenstumpf dreieckige Grundfläche
Volumen des Quaders:
V = int(z=0, a, int(y=0, b, int(x=0, c, 1)));
Volumen des Teilquaders bis zur Fläche:
V = int(z=0, a, int(y=0, b, int(x=0, c, cond)));
mit
cond = 1 wenn auf der einen Seite der Fläche, sonst 0.
Und "cond" sollte sich über die Normale definieren lassen, dann müsstest du das nur noch aufleiten.
Ansonsten, wenn du es anders lösen möchtest: Die grau markierte Fläche sieht mir so aus, als ginge sie von A nach C unten und von der Hälte der einen Kante zur Hälfte der anderen Kante oben.
EDIT:
Für Ebenenaufpunkt p und Ebenennormale n könnte "cond" in etwa so aussehen:
cond = 0.5 * (1 + sgn(dot(n, (x, y, z) - p)));
Also das mit cond habe ich nicht verstanden....Aber den anderen weg nicht
Beim anderen Weg kannst du schauen, was für Dreiecke/Vierecke du an den Seiten hast und darüber dich dann der Lösung annähern.
meine Vorgehensweise wäre:
- Gesamtvolumen Vges berechnen
- Flächen ABC (Grundfläche eines Teilkörpers) und die dazugehörige Deckfläche berechnen. Da die Hypothenusen der Deckfläche die Hälfte der Hypothenusen der Grundfläche betragen ist die Deckfläche 1/4 so groß wie die Grundfläche.
- Aus diesen beiden Flächen den Mittelwert bilden und diesen mit der Höhe multiplizieren. Du hast jezt das erste Teilvolumen V1 .
- Das errechnete Teilvolumen V1 von Vges abziehen und du hast das andere Teilvolumen V2 .
Tipp:
der vordere Teil ist eine Pyramidenstumpf
Kannst ihn aber auch als Prisma mit einer schrägen Fläche betrachten. Dan musst du aus der Grund- und Deckfläche den Mittelwert biden um zu einem volumengleichen Prisma zu kommen.
Genau, pyramidenstumpf hab ich gesehen. Nur was ist die Formel für das Volumen dann? Und pyramidenstumpf ist ja der rechte Teil pder