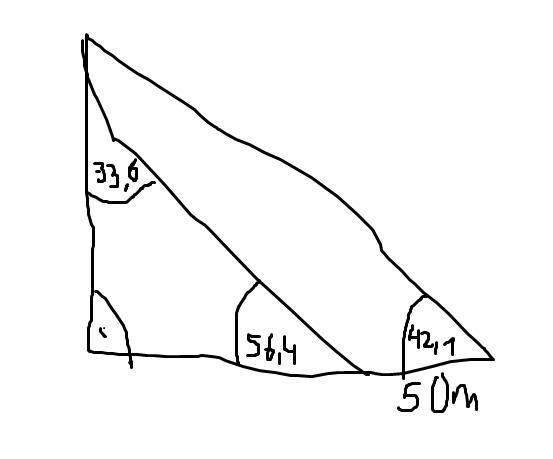
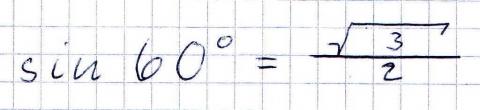TI-82 STATS Taschenrechner rechnet falsch!
Hallo, gerade wollte ich mir von dem Texas Instruments Taschenrechner den sinus ausrechnen lassen und dabei habe ich gemerkt dass etwas nicht stimmt. Eingegeben habe ich folgendes:. SIN 90 ENTER und herauskam 0.8939966636 usw. raus, dabei müsste es ja eins sein. was ist falsch eingestellt und wie wirds wieder normal? bei cosinus und tangenz ists das gleiche, sonst ist alles normal. Danke schonmal im Vorraus!!