Mathematik Integrieren?
Ich möchte eine Fläche zwischen zwei Funktionen ausrechnen.
Hierbei bilden die zwei Funktionen drei Schnittpunkte miteinander.
f(x)= x^3 und g(x)= x^2 + 2x
Wie genau rechne ich nun die Fläche aus?
Bei den Aufgaben zuvor, habe ich erfolgreich die zwei Schnittpunkte als Grenzen genutzt und einzeln mit f und g integriert und am Ende addiert. Nun weiß ich allerdings nicht mehr weiter, da diese Methode nicht mehr funktioniert, wenn man die höchste Grenze nutzt.
Es wird ausdrücklich von einer Fläche geredet.

Aufgabe d wird bearbeitet. Aufgabe b wurde nach genanntem Vorgehen erfolgreich gelöst.
Die a funktioniert auch nicht. Ich frage mich mit welchen Grenzen das Integral jeweils begrenzt gehört und warum es bei der b funktioniert hat beide Mal die gleichen Grenzen zu nutzen.
Hier der Aufschrieb

3 Antworten
Aufgabe d wird bearbeitet:
Wir berechnen zuerst die Schnittpunkte:
Ansatz: f(x) = g(x)
x^3 = x^2 + 2x
x^3 - x^2 - 2x = 0
x(x^2 - x - 2) = 0
x1= 0
x^2 - x - 2 = 0


Wir haben also 3 Schnittpunkte, wobei der mittlere die Fläche in zwei Teile teilt, die wir jeweils getrennt berechnen müssen:
Ansatz:
f(x) - g(x) = x^3 - x^2 - 2x


A = ⎜5/12⎜ + ⎜-8/3⎜ = 5/12 + 32/12 = 37/12



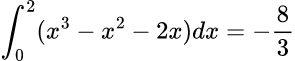
Schnittpunkte berechnen
korrekt. Habe ich gemacht.
dann die Grenzen nach einem Schaubild festlegen
Dazu braucht man aber einen Funktionenplotter. Kann man machen, muss man aber nicht. Die Grenzen sind immer durch die Schnittpunkte bestimmt. Bei 3 Schnittpunkten kann es nur einen linken, einen rechten und einen mittleren geben.
jedoch wurden die Funktionen f und g niemals subtrahiert:
Das kann ich mir kaum vorstellen. Ob man die vor dem Integrieren oder nach dem Integrieren subtrahiert, spielt keine Rolle. Beides ist möglich.
Es wurden die Integrale von d und g
Was ist d? Tippfehler?
Es wurden die Integrale von d und g mit unterschiedlichen Grenzen einzeln berechnet und dann am Ende addiert.
Das hört sich für mich nach "von hinten durch die Brust ins Auge" an. Kann es mir nicht si recht vorstellen, wie das funktionieren soll.
warum hat es bei der B dann doch geklappt?
Da du B verheimlichst, kann ich das nicht beurteilen.
Ja, ein Tippfehler : f meinte ich.
Ich füge kurz den Aufschrieb hinzu, der mich dahingehend verwirrt.
Ah ja. Da wird zuerst zwischen den Schnittpunkten jede Funktion einzeln integriert und die Ergebnisse werden voneinander abgezogen. Das ist die zweite Möglichkeit. Man kann auch zuerst die Funktionen voneinander abziehen und dann integrieren. Kommt aufs selbe raus.
Ich bevorzuge die Methode, dass man zuerst die Funktionen subtrahiert, weil man dann nur noch einmal und nicht zweimal integrieren muss.
Hat man mehrere Schnittpunkte, muss man diese Operation mehrmals machen und jedesmal von Schnittpunkt zu Schnittpunkt gehen. Hat man z.B. 5 Schnittpunkte, liegen dazwischen 4 Abschnitte, die man jeden einzeln berechnen muss und erst am Ende die Beträge addieren kann.
und dann am Ende addiert.
Hatte ich es mir doch gedacht. Da wird nix addiert. Auch in deinem Aufschrieb wird subtrahiert.
Ah okay also sind beide Methoden möglich… Wie müsste ich es dem Aufschrieb zu Folge bei drei Schnittpunkten berechnen? Also das von Schnittpunkt zu Schnittpunkt gehen… Gerade am Beispiel der Aufgabe d)
… ja, es wird subtrahiert: Ich habe aus Versehen den falschen Aufschrieb angeschaut, tut mir Leid.
Ah okay also sind beide Methoden möglich
Richtig.
Wie müsste ich es dem Aufschrieb zu Folge bei drei Schnittpunkten berechnen?
So wie du es bei zwei Schnittpunkten zwischen diesen beiden Schnittpunkten berechnest musst du bei mehreren Schnittpunkten jeden Abschnitt gesondert berechnen. Ich habs oben ja vorgemacht.
so sieht es aus


du kannst ganz normal von links bis 0 und von 0 bis rechts integrieren
egal , ob f(x) - g(x) oder umgekehrt , hauptsache es ist der Betrag
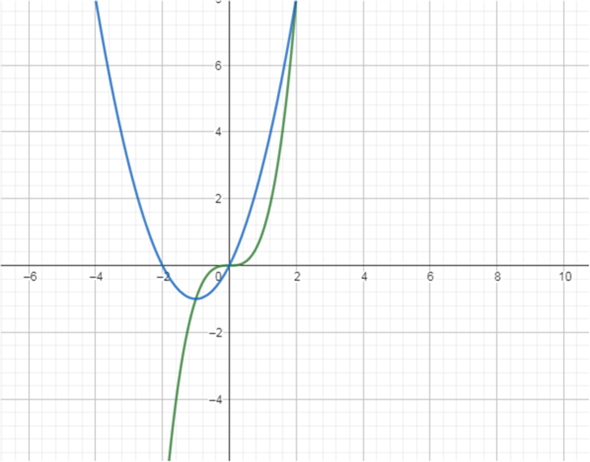

Danke für die Visualisierung.
Wenn ich solch ein Schaubild nicht habe, muss ich dann die Nullstellen der Graphen ausrechnen, um zu wissen welche Schnittpunkte überhaupt von Relevanz sind?
Berechne die 3 Schnittpunkte und berechne die Fläche dann wie in der anderen Aufgabe jeweils einmal für den kleinsten Schnittpunkt bis zum mittleren Schnittpunkt und einmal vom mittleren Schnittpunkt bis zum größten Schnittpunkt. Die beiden Flächen musst du am Ende dann noch addieren, um die Gesamtfläche zwischen den Funktionen zu bekommen.
Am Besten zeichnest du dir die Graphen der Funktionen auch nochmal in ein Koordinatensystem, dann siehst du auch die Flächen, die du berechnen musst.
Könntest du dir erklären, warum die a) nun nicht mehr funktioniert, obwohl hier auch nur zwei Schnittstellen existieren?
Sollte eigentlich funktionieren, was bekommst du als Ergebnis bei der a für die Integrale?
Ja genau passt doch, wenn du jetzt 104/3 - 120 berechnest und davon den Betrag nimmst, dann hast du die Fläche zwischen f und g.
Nein, musst du nicht. Du kannst f - g oder g - f berechnen, da die Fläche zwischen den Graphen der Betrag davon ist und das in beiden Fällen dann das selbe Ergebnis liefert
Stimmt tatsächlich…Bei der b habe ich am Ende allerdings auch beide Flächen miteinander addiert und kam zum Ergebnis. Warum also bei der a nun subtrahieren?
Bei der d) kommen bei mir 15/4 und 19/12 raus, da stimmt also etwas meinerseits nicht.
Ich werd eine Pause machen.
Du kannst die Funktionen auch vor dem Integrieren voneinander abziehen, dann ist die Rechnung eventuell etwas einfacher: Im Beispiel der a sähe das dann so aus:
1. Schnittpunkte berechnen:
x^2 - 1 = 15 --> x0 = -4 und x1 = 4
2. Integral von f - g bilden
f-g = x^2-1-15 = x^2-16
Integral ist dann x^3/3-16x
-4 einsetzen = -64/3+64
4 einsetzen = 64/3-64
Und dann die Differenz bilden
64/3-64+64/3-64 = 128/3-128=-256/3
Damit ist die Fläche dann 256/3
Wichtig ist f von g oder g von f abzuziehen und nicht zu addieren, auch bei der b.
Ich habe mein Problem, glaube ich nun durchhaut: Erst einmal habe ich den falschen Merkaufschrieb versucht zu verstehen, zweites aber haben wir das immer mit Visualisierungen gemacht: Das bedeutet wir wussten welche Funktion von welcher abzuziehen bzw. Wo die Grenzen zu setzen sind:
Vorgegangen wird hier so: Schnittpunkte berechnet und dann Fläche unter f minus Fläche unter g. Innerhalb der einzelnen Integrale wird allerdings zuvor nicht subtrahiert, nur am Ende. Muss man also bevor man die Grenzen einsetzt f und g voneinander abziehen, um die korrekten Werte zu erhalten?
Bei der b komme ich auf das richtige Ergebnis, indem ich am Ende addiere, bei der a korrekterweise, wenn ich subtrahiere… ich durchblicke diese Logik nicht
Was ist denn das richtige Ergebnis bei der B und welche Zahlen hast du dafür addiert?
Das Ergebnis soll 256/3 sein. Ich habe soeben addieren probiert, irgendetwas macht keinen Sinn.
meine Intervalle sind 40 und 8/3
8/3 passt, bei dem anderen Integral muss -40 rauskommen, da hast du vielleicht irgendwo einen Zahlendreher, und dann kannst du die Zahlen subtrahieren und kommst auf das richtige Ergebnis
Absolut korrekt, habe es gefunden. Ich danke für die Hilfe…
Vielen Dank!
Früher wurden diese Aufgaben uns immer so vorgerechnet: Schnittpunkte berechnen und dann die Grenzen nach einem Schaubild festlegen, jedoch wurden die Funktionen f und g niemals subtrahiert: Es wurden die Integrale von d und g mit unterschiedlichen Grenzen einzeln berechnet und dann am Ende addiert.
Wieso genau, ist dies hier nicht möglich bzw. warum hat es bei der B dann doch geklappt?