Partielle integration?

Kann mir jemand erklären wie ich hiervon die stammfunktion Bilde

20x*e^(-0,5)

Answer 1

[MichaelH77]

$f\left(x\right)=20x\cdot e^{\ -0.5x}$

$u=20x$ $u'=20$

$v'=e^{-0.5x}$ $v=-2e^{-0.5x}$

$u\cdot v-\int u'vdx$ $F\left(x\right)=20x\cdot\left(-2\right)e^{-0.5x}-\int20\cdot\left(-2\right)\cdot e^{-0.5x}dx+C$

$=-40x\cdot e^{-0.5x}+40\int e^{-0.5x}dx+C$ $F\left(x\right)=-40xe^{-0.5x}-80e^{-0.5x}+C$

$=-40\left(x+2\right)e^{-0.5x}+c$

https://www.math.tugraz.at/~lichtenegger/ananf5.pdf

Comments

[turnqueen2012]

Das sieht irgendwie kompliziert aus🫠

[Halbrecht]

@turnqueen2012

ist es auch . Aber geht es schneller ? Nein

[turnqueen2012]

@Halbrecht

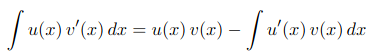
So war das eigentlich nicht gemeint. Hatte vorher selbst nur noch nie was von Ableitungen gesehen😅

[MichaelH77]

@turnqueen2012

Ableitungen und Integrale lernst du auch noch, wenn du Abi machst. Du bist erst 13. Dass es für dich so kompliziert aussieht, ist ganz normal

Answer 2

[hamberlona]

SweetDreams271 schrieb:

> 20x*e^(-0,5)

Das hab ich Dir doch vor knapp 2 Stunden schon beantwortet: klick

Für den Fall, dass Du Dich verschrieben hast und in Wirklichkeit 20x*e^(-0,5 x) meinst:

Zu integrieren ist 

20 x e^(-0.5 x)

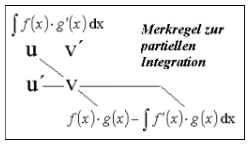
Nutzen wollen wir die partielle Integration:

Integral f'(x) g(x) dx = f(x) g(x) - Integral f(x) g'(x) dx

Das verbleibende Integral ist besonders einfach, wenn g'(x) eine Konstante ist.

Also legen wir fest: 

f'(x) = e^(-0.5 x) => f(x) = -2 e^(-0.5 x)

g(x) = 20 x => g'(x) = 20

und setzen dies ein 

f(x) g(x) - Integral f(x) g'(x) dx

= -2 e^(-0.5 x) * 20 x + Integral 2 e^(-0.5 x) * 20 dx

= -2 e^(-0.5 x) * 20 x + Integral 2 e^(-0.5 x) * 20 dx

= - 40 x e^(-0.5 x) + 40 Integral e^(-0.5 x) dx

= - 40 x e^(-0.5 x) - 80 e^(-0.5 x) 

= - 40 (x + 2) e^(-0.5 x)

Dieses unbestimmte Integral plus Integrationskonstante ist die Stammfunktion.

Kontrolle: Wenn wir das ableiten muss die Ausgangsfunktion herauskommen.

-40 ((x + 2) e^(-0.5 x))' 

= -40 ((x + 2)' e^(-0.5 x) + (x + 2) (e^(-0.5 x))')

= -40 (e^(-0.5 x) - 0.5 (x + 2) e^(-0.5 x))

= -40 (1 - 0.5 (x + 2)) e^(-0.5 x)

= 20 x e^(-0.5 x)