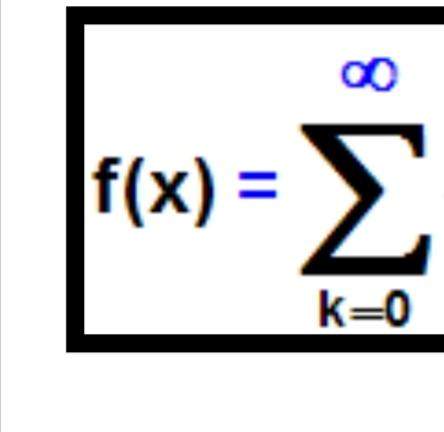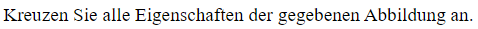Relation – die besten Beiträge

Folgende Aufgabe:

Meine Überlegungen:

a) Muss ich hier die Zahlen von 1-8 nehmen (M₈) und dann die Zahlen von 1-6 (M₆) und dann schaue ich für welche Zahlen aus der Menge M8 durch die Zahlen der Menge M6 ein k aus den natürlichen Zahlen entsteht?

Also 1:1 = 1; 2:1=2 ; 2:2 = 1, 3:1 = 3, 3:3 = 1; 4:1 = 2 ; 4:2 = 2 ; 4:4 = 1; 5:1 = 5 ; 5:5 = 1; 6:1 = 6 ; 6:2 = 3 ; 6:3 = 2 ; 6:6 = 1,

7:1 = 7; 8:1 = 8, 8:2 = 4; 8:4 = 2

Und diese müsste ich mit Pfeilen darstellen oder? Also von der 8 bspw. geht ein Pfeil zur 1,2 und 4. Habe ich das richtig verstanden?

b) reflexiv, weil x in Relation zu y steht

transitiv → die Begründung verstehe ich nicht :( bitte helfen!

es ist nicht symmetrisch, da ich die Reihenfolge nicht ändern kann. Hinsichtlich der vorgegebene Relation ist (6,1) nicht dasselbe wie (1,6) oder?

Folgende Aufgabe:

Kann mir jemand bei der Aufgabe helfen, weil ich irgendwie nicht weiß, was gemeint ist.

Wie zeichne ich einen Teilergraphen und wie würde der bei dieser Aufgabe aussehen?

Hallo,
in folgender Aufgabe seien auf RxR Relationen definiert.
Schon das "auf R x R" kommt mir spanisch vor, denn eigentlich bedeutet "auf" bereits, dass es es sich um eine Ebene handelt. "Auf R" wäre doch eigentlich korrekt. Soll man daraus schlussfolgern, dass man sich irgendwie im dreidimensionalen Raum befindet?
Dann die eigentliche Frage: was hat es mit diesem (x1, x2)R(y1, y2) auf sich? Soll man x1 und x2 als Koordinate in der R Ebene nehmen? So macht man das ja eig. bei Paaren. Das Problem ist aber, dass ja keinerlei Aussage über x2 und y2 existiert.
Bis jetzt gings immer nur um sowas wie xRy mit z.B. x < y - kein Problem.
Ich würde mir das gern in Gitternetzdarstellung skizzieren, jedoch komme ich dann bei allen auf eine vollständig gefüllte Ebene, bei der dann alle drei unten stehenden Eigenschaften gelten würden.

Gilt bei dieser Relation, welche auf N definiert ist die Alternativität, sprich vollständige oder unvollständige Ordnungsrelation? (Am besten mit Erklärung der Vorgehensweise :D)

a ∼ b:⇔ ∃ k ∈ N: a*k = b

Vielen Dank schonmal !

Ich brauche bitte eine Lösungsweg für diese zwei Aufgaben

Aufgabe 1

Auf der Menge N^2 wird eine Relation R erklärt durch (a, b)R(c, d) ⇔ a · d ≤ b · c

Ist R eine Quasiordnung, eine Äquivalenzrelation oder eine Ordnung? (Mit Nachweis)

Aufgabe 2

Es sei M die Menge der Menschen. Wir definieren die Relation R auf M durch:

xRy ⇔ y ist ein (nicht unbedingt direkter) Nachkomme von x oder y = x

Überprüfen Sie die Relation auf Reflexivität, Transitivität, Symmetrie und Antisymmetrie. (Mit Nachweis)

Kontext: Es liegt eine Relation vor, bei der (unter anderem) die 1 sowohl in Relation zu sich selbst, als auch in Relation zur 6 steht. Die Frage ist, ob die Relation eine Funktion definiert. Meine erste Vermutung war nein, aber mir stellt sich hier die Frage, ob es grundsätzlich möglich ist, dass eine Funktion an einer Stelle 2 Funktionswerte hat.

Und es in Pflanzenpflegeportalen oder sonstwelchen Pflegetipssquellen heißt dass sie diese nicht mögen/vetragen? Wenn man sie im Zimmer hat muss man ja ab und an lüften. Wenn die nun am Fenster stehen und dieses dans einzige ist zum Luftaustausch.... Wie reagiert die Pflanze ist das wirklich so schlimm für diese oder heißt das "nur" dass das Fester nicht permanet geöffnet sein sollte?

Guten Morgen,

ich habe eine Frage zu einer Datenbank-Übung, die ich gerade mache. Es geht darum, die Daten bis zur 3. NF zu untersuchen.

"Die Betriebsleitung beauftragt dich, die Verwaltung des Personals zu digitalisieren. Folgende Daten der Mitarbeiter werden erhoben: Vorname, Nachname, Geburtsdatum, Geschlecht, Wohnadresse, Anstellungsdatum, Gehaltsstufe, Abteilung, alle Gehälter mit Angabe des Datums der Auszahlungender Gehälter mit Gehaltsbetrag. Es soll möglich sein, die Karriere des Mitarbeiters in den Abteilungen, in denen er gearbeitet hat, zu verfolgen (mit Beginn des Abteilungswechsels)."

Mitarbeiter

Mitarbeiter_ID - PRIMARY KEY
Vorname
Nachname
Geburtsdatum
Geschlecht
PLZ
ORT
Straße
Hausnummer
Abteilung
Gehaltsstufe - FOREIGN KEY (Gehaltsstufe)
Datum_Auszahlung

Gehalt

Gehaltsstufe - PRIMARY KEY
Gehalt

Ist es richtig, dass es sich hierbei um eine 1 zu n Beziehung handelt?
1 Mitarbeiter hat 1 Gehalt.
1 Gehalt wird an n Mitarbeitern vergeben.

Ich glaube, dass ich die Normalisierung soweit richtig habe, bis auf das Attribut "Datum_Auszahlung".
Wäre es hier richtig, einen neuen Entitätstypen zu erstellen und Mitarbeiter_ID und Gehaltsstufe als Fremdschlüssel hinzuzufügen oder sollte man das Attribut entweder bei "Gehalt" oder "Mitarbeiter" hinzufügen?

Falls es noch andere Fehler in der Normalisierung gibt, wäre ich froh, wenn ich darüber informiert werde :).

Danke im Vorraus
Gruß Leyonad

Ich habe heraus gefunden, dass eine leere Menge nicht reflexiv ist. Angenommen es gibt eine Grundmenge A ={a,b,c} und R=∅. Ist R dann reflexiv, und wenn nein warum?

Also, die Frage wird so lauten: relate the diagram to the text.

Hallo, ich habe letztens dieses komische E-artige Zeichen in einer Mathematik Aufgabe gesehen und wollte wissen, was es bedeutet. Bestenfalls könnte das jemand leicht und verständlich erklären, da ich erst 14 Jahre alt bin und ich folglich noch nicht soo viel über Mathe weiß :)

Danke schon mal im Voraus für die Antworten! :D

ich habe noch eine Übung gemacht und möchte kurz checken lassen ob ich richtig liege mit einer Begründung. Falls ich falsch liege bitte korrigiert mich.

1. Hier habe ich surjektiv angekreuzt, da man mit (-2,-2), (2,-2) oder (0,0) auf 0 kommt. Hier bin ich mir nicht sicher, ob es injektiv ist um ehrlich zu sein.
2. Hier ist es bijektiv, da wegen x^2 nur positiven Zahlen rauskommen (=injektiv) aber auch (2,2) und (-2,2) man auf (4,0) kommt.
3. Hier ist es nur injektiv, da bei x nur positiven Zahlen kommen und nicht doppelt abbildet.
4. Auch hier ist das injektiv, da das Ergebnis hier auch nicht doppelt abgebildet werden kann, wegen den natürlichen Zahlen.
5. Hier ist es weder surjektiv noch injektiv, da wegen x^2 nur positive Zahlen rauskommen aber bei x^3 entweder - oder + Zahlen rauskommen. Somit kann man keine negativen Zahlen abbilden bei x.

Vielen Dank im Voraus.

f = {(1,4), (4,1), (2,3), (3,2)}

Was wäre denn dann die transitive Hülle? Ich dachte: Wenn man über Umwege hinkommt, muss man auch direkt hinkommen. Hier ist es doch jeweils nur ein hin und zurück. Also ich komme von 1 nur zur 4. Und das auf direktem Wege. So ist es auch bei den anderen -> transitiv





Falls euch das eine Zeichen nicht angezeigt wird, das ist ein "Element aus". Vielen Dank im voraus für eure Hilfe!

Moin,

ich studiere Informatik im ersten und bereite mich gerade auf meine erste Mathematik Klausur vor. Gerade bin ich bei Relationen / Äquivalenzrelationen und über folgende Beispiele gestoßen (s.Bild). Diese Beispiele sind aber lediglich geordnete Paare des Kreuzproduktes und ich verstehe nicht, wie man daraus die Transitivität ablesen soll?

Wenn eine konkrete Relation wie >= gegeben ist, kein Problem, aber hier keine Ahnung...

Hallo Leute,

ich bearbeite gerade eine Übung mit Relationen und muss bestimmen ob diese eine äquivalente Relation ist oder nicht. Leider bin ich mir nicht sicher, ob ich das richtig bearbeitet habe.

Äquivalenzrelation soll: Reflexiv, symmetrisch und transitiv sein!

Hier ist die Aufgabe:

Meine Ansätze:

(1): Keine Äquivalenzrelation, da nur (1, 1) und (-1, -1) geht. Da hier aber reele Zahlen sind klappt mit (2, 2) zum Beispiel nicht!

(2): Keine Äquivalenzrelation, da man hier eine negative und eine positive Zahl benötigt, um auf die 0 zu kommen (außer 0, 0). Zum Beispiel: (-2, 2) ist nicht reflexiv. (nicht sicher)

(3) Äquivalenzrelation, da alle Tupel entweder reflexiv, symmetrisch oder transitiv sind.

(4) Hier bin ich mir auch nicht sicher (habe trotzdem als Äquivalenzrelation angekreuzt), da man mit jeder negativen geraden Zahl und negativen geraden Zahl / negativen geraden Zahl und positiven geraden Zahl / positiven geraden Zahl genauso, wie mit den ungeraden Zahlen eine gerade Zahl bekommt, wenn man diese subtrahiert. Was wäre den mit (2, 3) zum Beispiel? Das ist schon mal nicht reflexiv.

(5) Äquivalenzrelation, weil surjektiv bedeutet, dass alle Elemente im Definitionsbereich auf alle Elemente im Wertebereich treffen müssen. Das geht hier, wenn man irgendeine natürliche Zahl einsetzt.

Stimmen die Ergebnisse? Wenn nein bitte korrigiert mich und klärt mich bitte auf. Bin gerade erst ins Thema eingestiegen.

Danke im Voraus.

Hey,

kann mir jemand bei den folgenden Aufgaben behilflich sein. Aufgabe 1 habe i h noch geschafft. Beim Rest hängt es etwas.

reicht es bei 1b) zu schreiben, dass „(P,(N),C_) ist eine geordnete Menge, für N >1 ist C keine totale Antwort?

ich weis es ist kein Hausaufgaben Forum hier, jedoch würde ich es nicht fragen wenn ich es wüsste und keine Hilfe brauchen würde.
danke vorab für jede hilfreiche Antwort

Wenn R eine Ordnungsrelation von MxM ist schreibt man die geordnete Menge (M,R). Aber wie schreibt man die geordnete Menge, wenn R eine Ordnungsrelation auf MxN ist?

Guten Tag liebe Leute,

ich beschäftige mich seit ca. 6 Monaten mit C# und seit ca einem Monat mit Datenbanken. Ich finde die Möglichkeiten, die .net anbietet relativ umfangreich, um nicht zu sagen verwirrend.

Bislang habe ich es zB so gemacht, per SQLConnection und SQLCommand Queries an eine lokale MS SQL Server DB zu senden.

Nun gibt es aber natürlich auch noch: DataSets, DataTables, TableAdapters, BindingSources, DataBindings und und und :)

Was ist die beste Möglichkeit zB eine rel. Datenbank mit 20 Relationen an ein Projekt und an meine Controls zu binden?

Macht man das über DataSets und BindingSources. Macht man das per Designer oder manuell?

Ich wäre für Tipps dankbar. Und vor allem auch für Links :)

Vielen Dank!