Geometrie – die besten Beiträge

Sehr geehrte Community,

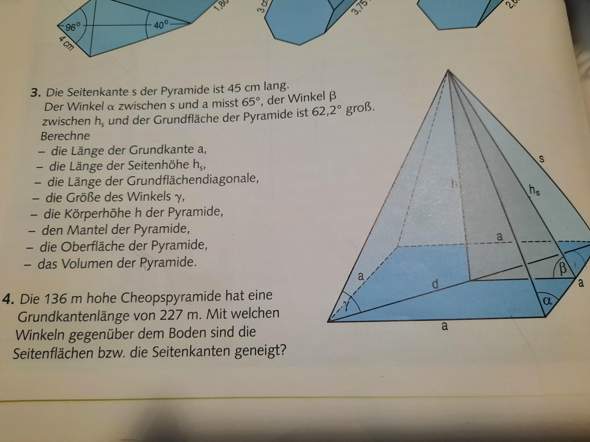
ich habe Schwierigkeiten bei der Aufgabe. Ich brauche nur Hilfe bei a, weil ich glaube mit Hilfe einer guten Erklärung würde ich es verstehen.

Ich würde mich freuen wenn jemand mir ein Feedback geben könnte.

Hallo

Beim stützvektor bei Aufgabe 3 kann man sich doch ein beliebigen Punkt E, F, oder S aussuchen? Aber da sind andere Koordinaten? Ich drehe gleich durch.

Ich hab zwar das lösungsheft aber ich versteh Aufgabe 7 trotzdem nicht

Sorry kann keine Fotos machen...

(Bild durch den Support entfernt)

„Ein Betonbalken (Breite 150 mm; Höhe 200 mm; Länge 525 mm) wird bei einer Stützweite von 450 mm auf Biegung beansprucht. Durch Lastaufbringung mit zwei gleichgroßen Schneidenlasten F/2 in den Drittelspunkten der Stützweite tritt bei einer Last F von 35 kN ein Versagen auf. Bestimmen Sie die Biegezugfestigkeit des Balkens“

Danke im Voraus!

Hallo,

Ich bekomme diese matheaufgabe einfach nicht hin. Kann mir jemand helfen?

Danke für alle Antworten

Es sei M der Mittelpunkt einer Strecke AB und g eine Gerade durch M.

Beweisen Sie : Der Abstand des Punktes A von g ist gleich dem Abstand des Punktes B von g.

Aufgabe:

In einer quadratischen Pyramide ist der Diagonalschnitt ein gleichseitiges Dreieck mit der Seitenlänge 21,2cm. Berechne das Volumen der Pyramide und den Winkel zwischen der Seitenfläche und der Grundfläche.

Wie kann ich a und h Berechnen?

Vielen Dank im Voraus!

Kann mir jmd bei Aufgabe 8c,d und 12 helfen?

Guten Abend allerseits,

Und zwar verwirrt much die Aufgabe Nr.3...Die Dreiecke in der Pyramide sind nicht rechtwinklig, soll ich den den Satz des Pythagoras einsetzen? Wenn ja, wie?

Ich habe für die Grundkante 434m raus, 45m für die Seitenhöhe und 614m für die Grunddiagonale.Weiter komme ich nicht.

Das Volumen eines Quaders ist 3750cm^3. Die Grundfläche ist um 10cm länger als breit, die Höhe des Körpers beträgt 10cm. Berechne die Länge und Breite der Grundfläche. Wie soll das gehen wenn man nur die Höhe hat??

Ich hätte C und D gesagt weil 2 Ecken und 5 Ecken und 3 und 4 also 2,3,4,5

Kreis anstatt Mond macht doch keinen Sinn?

ansonsten würde ich höchstens sagen A und D

3 Ecken auf 4 und 4 auf 5

was stimmt jetzt ?

Kann jemand mir dabei bitte helfen - Aufgabe 10

Ich hab hab seit ne ganze Stunde Probleme mit diese eine Aufgabe. ich weis net ob sich um Trapezprisma oder halbe Pyramide handelt jedoch hab versucht und das kam raus

Volume von Quader und ^trapezprisma ^

V_gesamt = 336cm^3

oberfläche von Q und ^Tp^

O_gesamt =371,64cm^2

kann mir jmd bitte sagen ob das stimmt oder nicht falls nicht was hab ich falsch ?

Danke im Voraus

So kompliziert formuliert.

hiii, ich brauche hilfe bei dieser Aufgabe.

also nh ich will nicht die lösung sondern verstehen wie man das rausbekommt

dankeschööön für eure hilfe