Graphen?

Kann jemand mir dabei bitte helfen - Aufgabe 10
3 Antworten

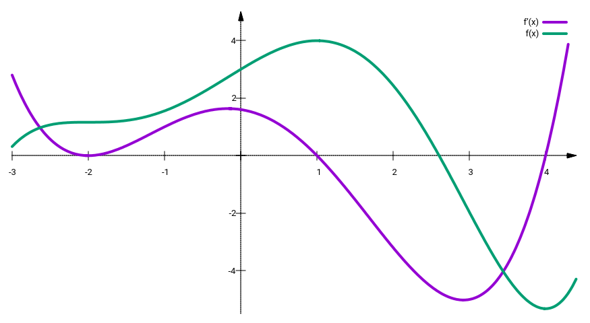
Die violette Kurve ist die Ableitung f’(x), die Du hast, und die grüne ist eine mögliche Wahl für f(x). Du siehst Dir jetzt die violette Kurve an, identifizierst alle interessanten Punkte und überlegst Dir, das die für f(x) bedeuten.
- An x=−2 hat f’(x) eine Nullstelle, die gleichzeitig auch ein Minimum ist. Daher hat f(x) an dieser Stelle einen Wendepunkt mit horizontaler Wendetangente
- An x≈−0.1712 hat f’(x) einen Extrempunkt (Maximum), daher hat f(x) dort einen Wendepunkt.
- An x=1 hat f’(x) eine Nullstelle bei fallender Monotonität, daher hat f(x) dort ein Maximum.
- An x≈2.9212 hat f’(x) einen Extermpunkt (Minimum), deshalb hat f(x) dort einen Wendepunkt.
- An x=4 hat f’(x) eine Nullstelle bei steigender Monotonität, daher hat f(x) dort ein Minumum.
Vermutlich nicht, weil ich nicht weiß, was Geogebra sein soll.
Ahhh, womit hast die die Graphen gemacht?
Mit Gnuplot. Dazu habe ich einfach Deine Funktion anhand der Nullstellen als (x+4)²⋅(x−1)⋅(x−4) geschätzt, und dann festgestellt, daß ich noch ⅒ davorschreiben muß, damit es zu Deinem Bild paßt. Dann habe ich das Zeug ausmultipliziert ( ⇒ x⁴−x³−12x²−4x+16) und zuletzt noch integriert (= die Funktion gesucht, deren Ableitung das ist was dasteht). Dann geplottet und noch ein paar Feinadjustierungen vorgenommen:
plot [-3:4.4] [-5.5:5] (x<4.3)?(x**4 -x**3 -12*x**2 -4*x+16)/10:NaN lw 4 title "f’(x)", (x**5/5 -x**4/4 -12*x**3/3 -4*x**2/2 +16*x )/10+3 lw 4 title "f(x)"
Schau dir an, wo f' eine Nullstelle hat. Ist dort zusätzlich eine Vorzeichenwechsel von f', dann ist dort ein Extemum. Ist dort kein Vorzeichenwechsel, so ist dort ein Sattelpunkt.
du musst dir einfach überlegen was extrempunkt in der ableitungsfunktion bedeutet (nämlich immer f‘(x)= null) das heißt in der ableitungsfunktion hat der graph an der stelle einen schnittpunkt mit der x achse und läuft je nach art des extrempunkts von negativ zu positiv oder andersrum
wendepunkt bedeutet glaube ich steigung 0 am graph von f‘
Ich verstehe die Aufgabe jetzt allgemein nicht und was ich jetzt begründen soll/wie ich begründen soll , da ich nicht mal Aussagen habe.
also die ableitungsfunktion die man hier sehen kann beschreibt ja die steigung der originalfunktion
beispiel:
nullstelle in der ableitungsfunktion bedeutet extrempunkt in der originalfunktion
deine begründung könnte jetzt sein bei x=2 liegt ein extrempunkt vor da der graph von f‘ dort eine nullstelle hat
des weiteren handelt es sich bei der extremstelle um ein Maximum da der Graph f‘ von positiv nach negativ läuft( in der Originalfunktion heißt das er steigt erst und dann fällt er /\ also ein Hochpunkt)
und das machst du jetzt bei jeder nullstelle
wichtig ist das nicht die nullstelle allein ausschlaggebend für eine hoch unter tiefpunkt ist du musst dir genauso den verlauf anschauen bei x=-2 zum beispiel liegt kein vorzeichenwechsel vor in der originalfunktion äußert sich das dann so das der graph erst steigt und kurz gerade läuft und dann nochmal steigt man spricht da auch von einem terrassenpunkt
wendepunkte liegen immer vor wenn der graph der ableitungsfunktion steigung 0 hat wie zum beispiel bei x ≈3 (man kanns nicht richtig ablesen
Kannst du mir bitte sagen , was ich bei Geogebra eingeben soll , damit ich so welche Graphen zusehen bekomme.