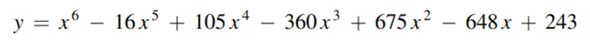Ableitung – die besten Beiträge

Ich suche, wie man die HP, TP und W einer Funktionenschar berechnet, aber der Parameter schon vorgegeben ist.

Beispiel: ft(x)=x^3-3t*x^2+1

t=1,5

Wie gehe ich vor? Ich konnte nichts im Internet finden, deshalb frage ich euch :)

LG

Ich wollte das Volumen einer Kugel beschreiben, wobei der Radius in x Richtung doppelt so groß ist wie der Radius in y Richtung.

Ich hatte die Idee, das Volumen einer Kugel mit einem dreifachen Integral darzustellen, wobei der Radius aber in x Richtung doppelt so große ist wie in y Richtung . Also ich den Radius als Vektor mit x und y Komponente darstelle.

Jetzt ist mein Problem, dass ich nicht weiß wie und ob man Vektoren integrieren kann.

vllt ist meine Idee auch müll, ich wollte es nur mal ausprobieren

Aufgabenstellung

was ich bisher habe (😔)

Wie soll ich das angehen? ich habe wirklich keine ahnung

LG und danke

Hallo, bitte um schnelle Antwort!

Wie kann ich

2 durch wurzel x

und

wurzel x durch 2

umschreiben?

Danke!

Ich komme nicht weiter bei der roten und blauen Parabel. Die grüne habe ich bereits.. Bitte kann mir wer die Lösungen geben?? Die Rechnungen verstehe ich viel besser. Ich bin momentan total im Stress..

Forme f(x)= x²+6x+6 in die Scheitelpunktform und beschreibe dein Vorgehen.

Forme die Scheitelpunktform um und gib die Koordinaten des Scheitelpunkts an:

a)y=4x²+24x-9

b) y=6+1/2x²-2x

c)y=-3x²-9x

Was muss ich hier machen? Weil erst bei e steht dass man die h Methode anwenden muss aber was musste ich davor machen?

Gegeben sei weiterhin die Gerade: h(x)= x-2. Bestimmen Sie für welche Werte des Parameters a die Gerade h sekante von gf(x) ist.

Muss ich da was einsetzen??

??

1. ∇ × (∇f) = 0. -> "Gradientenfelder sind Wirbelfrei"
2. ∇ · (∇ × v) = 0 -> "Wirbelfelder sind Quellfrei"

was heißt das "auf deutsch", also geometrisch? was kann ich mir darunter vorstellen wenn ein Gradfeld jetzt wirbelfrei ist`?

Hallo,

ist es möglich, folgende Aufgabe mit dem Taschenrechner (Casio fx-991DE X CLASSWIZ) zur lösen?

Bestimmen Sie die Nullstellen der ersten und zweiten Ableitung von f(x) = x³ - 9x² + 24x + 2. Überprüfen Sie ob es sich bei den Nullstellen um Maxima, Minima oder Wendepunkte handelt.

Ich checks nicht.

Ich checke generell ned wofür ich den Grenzwert bestimmen soll und was dad bedeutet.

Wie löst man diese Aufgabe?

Bitte helft mir, ich kriege diese Aufgabe nicht hin, man muss die Ableitung mit der Kettenregel lösen, ich glaube die Teilableitungen sind bei der äußeren Funktion 3 und bei der inneren Funktion 1/2 (2-x)^1/2. Die Formel, um alles zusammenzurechnen ist f'(g(x))*g'(x)

(f ist äußere Funktion, g ist innere Funktion)

Hallo Zusammen,

ich habe eine Frage zur folgenden Aufgabe:

Zeige dass folgende Funktion an der Stelle y(3) einen Sattelpunkt besitzt:

.

Mir ist klar, dass ein Sattelpunkt ein spezieller Wendepunkt ist, der in diesem Fall bei y(3) keine Steigung hat und somit bei der ersten Ableitung = 0 sein muss.

Die weiteren Definitionspunkte der Sattel- bzw. Wendepunkte sind meines Wissens nach, dass die zweite Ableitung gleich = 0 sein muss und die dritte Ableitung ungleich 0.
In der oben erwähnten Aufgabe sind allerdings, gemäss Lösung, die ersten 4 Ableitungen = 0 und erst die 5. ungleich 0.
Weshalb handelt es sich dann trotzdem um einen Sattelpunkt? Ich dachte die dritte Ableitung muss ungleich 0 sein?

Wie gehe ich da vor. Muss ich die Punkte einfach nur für a und b einsetzen?? Sind das alles normalparabeln?? Danke im voraus für eure Hilfe ihr lieben

Die Punkte O(0/0), P(5/0), Q(5/f(5)), R(u/f(u)) und S(0/f(0)) des Graphen von f mit f(x)=-0,05x^3+x+4; 0<= x <= 5 bilden ein Fünfeck. Für welches u wird sein Flächeninhalt maximal?

Hallo

ich übe gerade für die ma Arbeit und Check den grundsetzungsverfahren nich also die beiden Gleichungen sind 1: 7x-2y=4 2: 3x-y=11 ich muss ja eig die x wegmachen und das geht ja theoretisch mit der zweiten Gleichung aber mit der anderen steht dann 2y=4 und ich weiß nicht weiter oder ob das so richtig erstmal ist

danke im Voraus

Wie löst man diese Aufgabe ?

Mein Ansatz:

A) mit 1. Ableitung hochpunkt berechnen. Für breite die Nullstellen und somit Abstand berechnen.

B) steigungswinkel and den Nullstellen bestimmen.

C) vielleicht steigungsdreieck einzeichnen bei dem beide Seiten 1 LE lang sind, denn das ergibt einen Winkel von 45 Grad?? Aber weiter weiß ich nicht.

Wie löst man diese Aufgabe ?