Wie geht man an dieses Mathe-Problem ran und was wäre die Lösung?
Die Punkte O(0/0), P(5/0), Q(5/f(5)), R(u/f(u)) und S(0/f(0)) des Graphen von f mit f(x)=-0,05x^3+x+4; 0<= x <= 5 bilden ein Fünfeck. Für welches u wird sein Flächeninhalt maximal?
3 Antworten
Die Punkte O,P,Q,S sind festgelegt, nur der Punkt R hängt von u und f(u) ab.
Die grüne Linie ist der Graph von f(u).
R kann sich auf der grünen Linie zwischen S und Q bewegen.
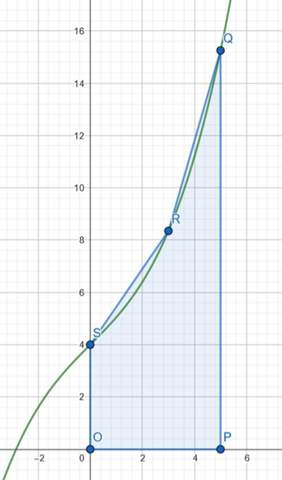
Man erkennt leicht, dass das blaue Fläche dann am grössten ist, wenn der Punkt R mit S oder Q zusammenfällt. Das ist für u = 0 oder u = 5 der Fall.
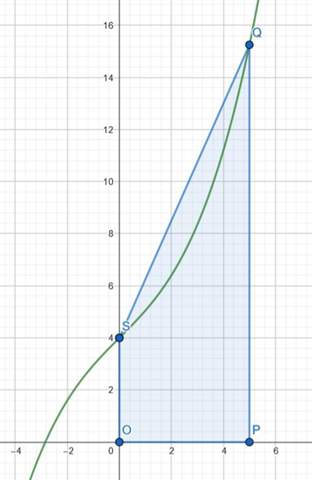
Dazu muss man beweisen, dass der Verlauf der Geraden S-Q im Intervall [0,5] grösser ist als f(x).
Geradengleichung von S-Q: g(x) = 2.25x + 4
g(x) - f(x) >= 0 im Intervall [0,5] ?
g(x) - f(x) = 2.25x + 4 - (0.05x^3 +x +4)
g(x) - f(x) = 1.25x - 0.05x^3
g(x) - f(x) = x(1.25 - 0.05x^2)
Wegen x >= 0 muss gelten
1.25 - 0.05x^2 > 0
bzw.
25 - x^2 > 0
Das ist für x € [0,5] der Fall.
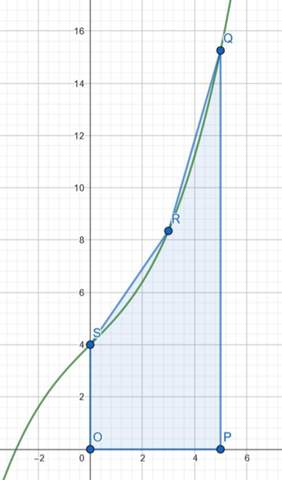
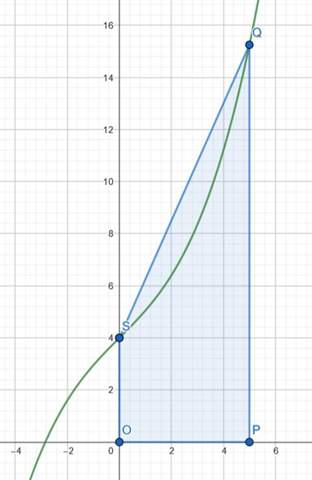
Ich kann dir dabei nicht helfen. Aber daran sieht man perfekt was die Lehrer in den Schulen so treiben.
Einmal über drüber unverständlich erklärt und Danach folgt nur noch "Ist doch nicht mein Problem.".
Das sind übrigens auch die Typen die behaupten:"Die Noten sind so schlecht weil die alle dumm sind."
Leider wahr. Der Mathe-Unterricht sollte sich auf wenige grundsätzliche Themen beschränken. Nur interessierte Schüler sollte man mit solchen Aufgaben konfrontieren.
Hier ist es wichtig, eine Skizze zu zeichnen und sich die Situation grafisch zu veranschaulichen. Am besten zeichnet man sie für zwei Werte von u (zum Beispiel u=1 und u=2), um zu sehen, was sich am Fünfeck ändert, wenn man u verändert.
Dann stellt man mithilfe von geometrischen Flächenformeln einen Ausdruck für den Flächeninhalt des Fünfecks auf. Nachdem es keine Formel speziell für Fünfecke gibt, wird man das Fünfeck in einfachere Teilflächen zerlegen und dann den Gesamtflächeninhalt aus deren Flächeninhalten aufbauen.
Wenn man dann die Funktion A(u) des Flächeninhalts A hat, ist es ein gewöhnliches Optimierungsproblem, bei dem man das Maximum der Funktion A sucht.
Was ist das denn für ein Rant? Nur weil jemand um einen Tipp für eine Hausaufgabe fragt, heißt es noch nicht, dass die Person keinen guten Unterricht hatte!