Wie löst man diese Aufgabe?
Ich sitze schon locker eine halbe stunde daran und komme nicht weiter, kann mir jemand helfen?
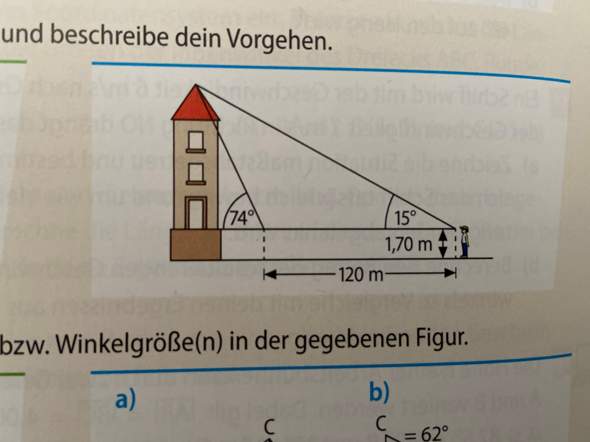
Die blaue die ganz zu sehen ist meine ich
mit der tangens, sinus und cosinus und so muss man die höhe des Gebäudes ausrechnen, und falls es irgendwie hilfreich ist, das habe ich schon dazu gemacht
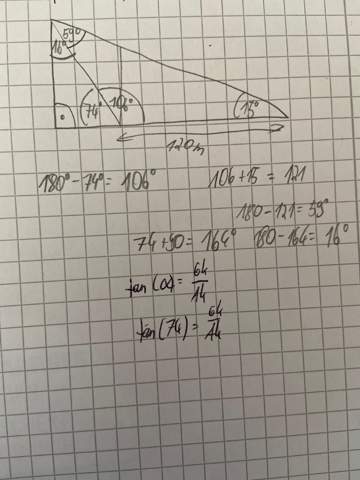
Weiter komme ich wirklich nicht, kann mir jemand helfen?
3 Antworten
Hier zwei Lösungen zu dem Problem:
Zuerst die Skizze (musst Du natürlich drehen, damit es mit Deiner übereinstimmt)
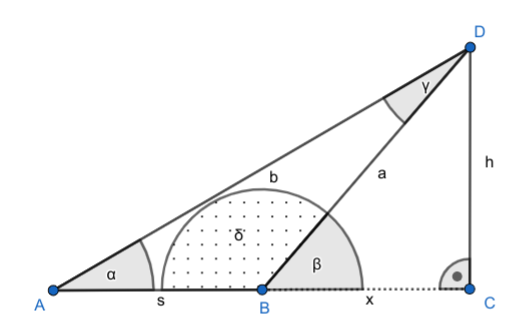
Und hier die beiden Lösungswege (einmal wird nur der Tangens benutzt und auf dem rechts abgebildeten Weg wird der Sinussatz verwendet):

Du musst nur am Ende noch 1,70 m addieren.
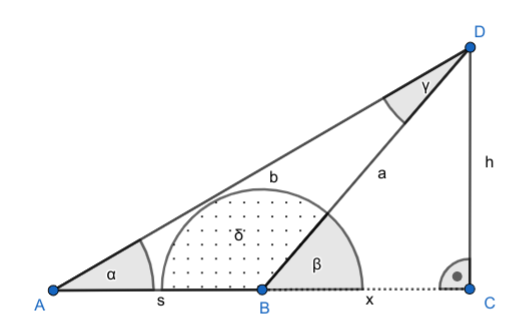

aber wie kann ich denn h bestimmen wenn ich mit x und h zwei variablen habe?
Die Gleichungen von gauss58
(1) h / (x + 120) = tan(15°)
(2) h / x = tan(74°)
kannst du beide nach h umstellen. Multipliziere beide Gleichungen mit dem Nenner. Bei der ersten Gleichung mit ( x + 120 ) multiplizieren und bei der zweiten Gleichung mit x multiplizieren. Dann hast du:
(1) h = (x + 120) * tan(15°)
(2) h = x tan(74°)
Du kannst jetzt das Gleichsetzungsverfa hren anwenden. Dazu werden beide Gleichungen gleichgesetzt:
(x + 120) * tan(15°) = x tan(74°)
Die kannst du jetzt nach x auflösen.
h bekommst du dann später wenn du deine Lösung für x in eine der Gleichungen einsetzt und nach h umstellst.
Du kannst zweimal den Tangens anwenden. In Deinem Dreieck mit den Winkeln 16°, 74° und 90° ist die Höhe h gesucht und die Grundseite nenne ich x. Dann gilt:
(1) h / (x + 120) = tan(15°)
(2) h / x = tan(74°)
----------------------
Nach x umstellen, gleichsetzen und h bestimmen.
Nicht vergessen, die Standhöhe von 1,70 m zu addieren.
aber wie kann ich denn h bestimmen wenn ich mit x und h zwei variablen habe?