Ist mein Dreieck Sinus, Tangens oder Cosinus?
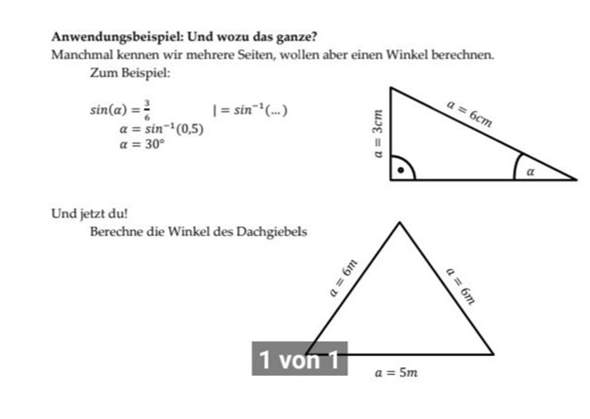
Hallo Leute. Ich muss das untere Dreieck berechnen. Habe schon mal 5:6 gemacht aber ich muss ja nach cos., tan., oder sinus ausrechnen aber weiß nicht woher man weiß, was es ist.
4 Antworten
Die Aufgabe ist etwas schwer gestaltet. Beachte dass du den Sinus, kosinus und tangens nur im Rechtwinkligen Dreieck benutzen darfst
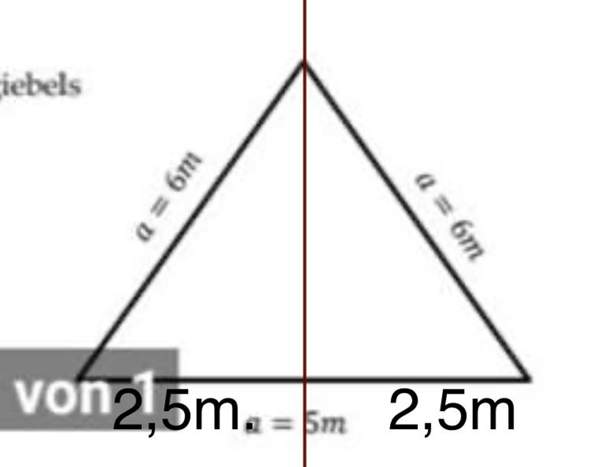
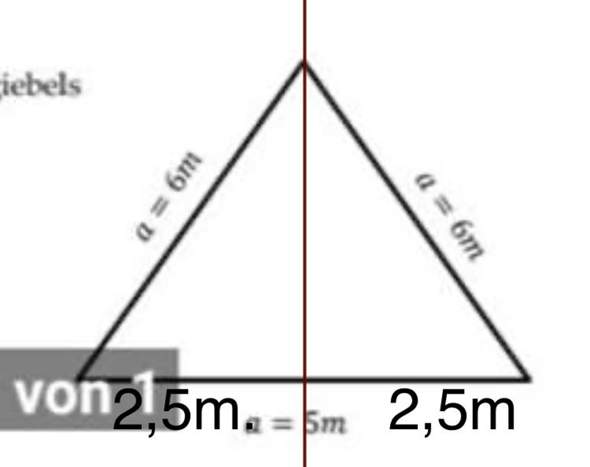
deswegen musst du das Dreieck in zwei rechtwinklige Dreiecke teilen. das machst du indem du eine gerade von der oberen Spitze geradeaus nach unten auf den Mittelpunkt der 5cm langen Seite ziehst. Damit hast du zwei neue Dreiecke und kannst so die Winkel ausrechnen.
bei weiteren Fragen einfach melden 🙋🏽♂️
du kannst dich übrigens immer melden bei mir. Habe das Thema dieses Schuljahr durchgenommen und auch arbeiten zum üben wenn du brauchst
Sinus & Co können nur bei rechtwinkligen Dreiecken abgewendet werden, also würde ich eine Winkelhalbierende von der oberen Spitze des Dreiecks nach unten machen, so dass die untere Strecke (5) halbiert wird und ein (bzw. zwei) rechte Winkel entstehen
Sinus = Gegenkathete : Hypotenuse
Kosinus = Ankathete : Hypotenuse
Tangens = Gegenkathete : Ankathete
Die Höhe des neu entstandenen Dreiecks haben wir nicht, deshalb nehmen wir die anderen beiden Strecken, die 2,5 und die 6, also die Ankathete und die Hypotenuse. - > Kosinus!
Die Aufgabe ist etwas fies gestellt, denn das gegebene Dreieck ist gar nicht rechtwinklig. In so einem Dreieck gibt es weder sin, noch cos noch tan.
Aber du kannst eine Höhe einzeichnen und zerlegst so dein Dreieck in zwei rechtwinklige. Versuch das mal! Kommst du damit weiter?
Und wie rechnet man denn bei Dreiecken, die nicht rechtwinklig sind.
Danke
Bei Dreiecken, die nicht rechtwinklig sind, nutzt man den Sinus- oder Kosinussatz, aber diese Sätze lernst du, falls überhaupt, erst viel später (sie sind bei manchen Bundesländern und Schulformen im Lehrplan und bei anderen nicht).
Weißt du denn, was eine Höhe ist?
An der Ecke, an der die zwei 6m langen Seiten zusammenlaufen eine Linie senkrecht auf die untere Linie zeichen. Dann hast du ein rechtwinklige Dreieck.
Mit den Kosinussätzen kannst du auch dieses nicht rechtwinklige Dreieck berechnen.
a^2 = b^2 + c^2 - 2*b*c*cos alpha bzw. die weiteren beiden analog dazu.
Da dir drei Seiten gegeben sind und auch ein gleichschenkliches Dreieck hast, sind die beiden Dachwinkel unten gleich groß.
Ich frage mich gerade auch, warum alle drei Seiten mit a bezeichnet werden, anstatt mit a, b, c?
Was meinst Du mit Höhe einzeichnen?
Ein anderes Dreieck zeichnen?
Du zeichnest eine Linie von der oberen Spitze senkrecht nach unten auf den Mittelpunkt der 5cm langen Seite.
dann hast du das dreieck in zwei rechtwinklige Dreiecke geteilt.
im unteren Dreieck hast du ja noch keinen rechten Winkel; daher musst du die Höhe einzeichnen und mit Pythagoras berechnen; dann zB sin alpha = h/6
Kann es sein dass Sie den cos alpha meinen. Bei Anwendung des sin muss die Höhe nämlich nicht berechnet werden.
Danke!!