Satz des Pythagoras?
Ich komme gerade nicht weiter. Ich habe bis jetzt zu der Aufgabe das:

Ich habe also jetzt oben das Dreieck und habe aber beim unteren Teil nur einen Wert, und zwar die Kathete 4,25 cm. Wie soll ich es jetzt mit einem Wert berechnen, wie lang f2 ist und die andere Seite?

Ich habe jetzt in das Teildreieck nochmal die Höhe eingezeichnet (kam mir so in den Kopf) und habe jetzt raus, dass die Seite 3,01 cm lang ist und man so jetzt auch f2 berechnen könnte. Ist das richtig?
in das Teildreieck
Welches?
Habt ihr Winkelfunktionen zu Verfügung?
Unten, also ist ja egal welches. Ne, wir haben wirklich nur Satz des Pythagoras, Kathetensatz und Höhensatz, also wir können keine Winkelfunktionen benutzen
3 Antworten
P.S.: Da stand vorher etwas komplett Falsches, weil ich aus irgendeinem Grund gedacht hatte, der Winkel bei D wäre ein rechter.
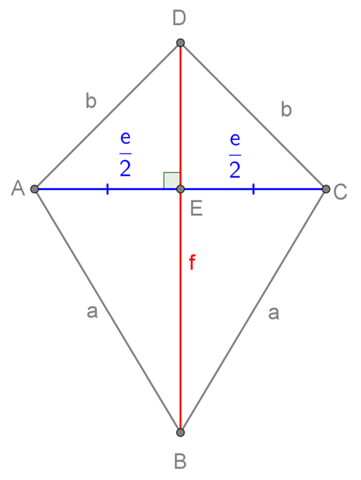
Dein Deltoid sieht also ungefähr so aus:

Bei jedem Deltoid stehen die Diagonalen e und f normal aufeinander, bei Dir sind zusätzlich noch die Winkel bei A und C (also α und γ) gleich 90°.
- Die Diagonale f besteht aus zwei Teilen: Einem oberen (ich nenne ihn f₁) über dem Schnittpunkt mit e und einem unteren, f₂, unter dem Schnittpunkt mit e.
- Den unteren Abschnitt der Diagonale f₂ bekommst Du aus einem rechtwinkeligen Dreieck, in dem er Kathete ist: f₂² + (½e)² = a² ⇒ f₂=√(a²−¼e²)≈5.8
- Für den oberen Abschnitt von f können wir zwar aufschreiben ¼e²+f₁²=b², aber das hilft nicht viel weiter, weil wir ja aus einer Gleichung nicht zwei Unbekannte (f₁,b) ausrechnen können.
- Andererseits können wir für die linke Hälfte des Deltoids aufschreiben f²=a²+b² und daraus das b²=f²−a² isolieren
- Das fassen wir mit der vorigen Gleichung zusammen und bekommen ¼e²+f₁²=f²−a², da ersetzen wir f=f₁+f₂ ein und bekommen ¼e²+f₁²=(f₁+f₂)²−a²=f₁²+2f₁f₂+f₂²−a². Darin hebt sich das f₁² weg, und wir bekommen ¼e²=2f₁f₂+f₂²−a². Da wir f₂ schon kennen, erhalten wir f₁=(¼e²−f₂²+a²)/(2f₂)=3.1
- Die Diagonale f=f₁+f₂=8.9
- Bei allen Vierecken, deren Diagonalen aufeinander normal stehen, bekommt man den Flächeninhalt sofort als A=½ef=37.9
- Jetzt können wir und auch gemütlich das b ausrechnen, b=√(f²−a²)=5.3
- Der Umfang ist natürlich einfach U=2a+2b=24.9
2.P.S.: Da in der Diskussion Zweifel daran aufgetaucht sind, ob die Diagonale e zwischen A und C liegt oder zwischen B und D, rechne ich das Beispiel nochmals unter der anderen Annahme durch. Dazu verwende ich dieselbe Skizze wie oben, schreibe aber einfach die Angabe um: a=7.2 und f=8.5, außerdem natürlich α=γ=90°. Immer wenn ich im folgenden von f schreibe, meine ich das, was in Deiner Angabe „e“ heißt.
- in diesem Fall verrät uns die rechte Hälfte des Dreiecks f²=a²+b² ⇒ b=√(f²−a²)=4.5
- Damit haben wir sofort den Umfang U=2a+2b=23.4
- Wir zerlegen wieder die Diagonale f in f₁ (oben) und f₂ (unten), f=f₁+f₂
- Das linke obere Dreieck verrät uns b²=¼e²+f₁²
- Das linke untere Dreieck verrät und a²=¼e²+f₂²
- In der letzteren Gleichung ersetzen wir f₂=f−f₁ und erhalten a²=¼e²+f²−2ff₁+f₁²
- Wenn wir jetzt die beiden Gleichungen b²=¼e²+f₁² und a²=¼e²+f²−2ff₁+f₁² voneinander subtrahieren, bekommen wir b²−a²=2ff₁−f², und daraus können wir f₁ leicht berechnen: f₁=(f²+b²−a²)/(2f)=2.4
- Daraus können wir leicht e berechnen (linkes oberes Dreieck): b²=¼e²+f₁² ⇒ e=2√(b²−f₁²)=7.7
- Und jetzt bekommen wir auch den Flächeninhalt: A=½ef=32.5
wie beschriften ` ganz und gar nicht
mein Bild ist an Wikepedia orientiert ( was nicht allgemein gültig sein muss )
aber ich kenne e nur als die lange Diagonale
Ich habe mich in der Skizze verschaut und tippe gerade die richtige Antwort ein.
Meiner Meinung nach sollte e zwischen den Punkten A und C liegen
hast du ein beschriftetes Deltoid in deinen Unterlagen ? Was ist da e , was f ?
Ich habe jetzt auch die andere Interpretation der Angabe durchgerechnet.
f1 Hast du berechnet.
f² = 7,2² + |AB|²
(f-f1)² + 4,25² = |AB|²
Damitlässt sich AB und f berechnen.
Man muss sich vor allem erstmal über die Seitenbezeichnungen verständigen !

Da lt. Angabe die Winkel bei A und C gleich 90° sind, und e wahrscheinlich (!) zwischen A und C liegt, nehme ich an, daß in diesem Fall wohl die Diagonale f die Symmetrieachse des Deltoids ist, nicht wie in Deiner Skizze e.
das ist gut möglich wegen der gegebenen Infos
Aber das ist eben ein Problem
die FS muss also wissen was in ihrer glorreichen Erziehungsanstalt bzw im Buch Sache ist
Ist es nicht egal, wie man es benennt? Mir wurde gesagt, es sei egal und es gibt ja zum Beispiel auch Drachen, wo es nicht ABCD ist, sondern NHGJ oder sowas
Man muß wissen, ob e zwischen A und C oder zwischen B und D liegen soll. Meiner Meinung ist nur ersteres sinnvoll, weil A im Alphabet vor B kommt und e vor f. Auch die deutsche Wikipedia handhabt das so: e=AC, f=BD
Allerdings ist das Deltoid bei Wikipedia so gezeichnet, daß die beiden gleichen Winkel bei B und D liegen (also β=δ), während bei Dir α=γ gilt. Bei Wikipedia ist also AC=e die Symmetrieachse des Deltoid, bei Dir muß sie BD sein, und ich habe in meiner Antwort angenommen, daß in Deiner Angabe e=AC und f=BD, was dann f zur Symmetriechase macht.
genau das ist das Problem
Das Netz ist voll von Drachen, die mal so , mal so bezeichnet sind .
Es kommt bei der Bezeichnung ja schon darauf an , ob man den Drachen mit einer senkrechten oder waagrechten Symmetrieachse zeichnet
Und nur die FS kann wissen , was bei ihr gilt
Ich verstehe jetzt nicht ganz.. bei mir ist a sozusagen b hier. Spielt das eine Rolle? Ich dachte, es wäre egal, wie man es beschriftet.