Hilfe bei Physik Aufgaben zu elektrischen Schwingkreisen?
Könnt ihr mir bei folgenden Aufgaben helfen? Ich bin da dezent überfordert:
Skizziere den Aufbau eines einfachen elektromagnetischen Schwingkreis bestehend aus
einem Kondensator und einer Spule.
• Skizziere, beschreibe und erkläre den Verlauf einer Periode eines elektrichen
Schwingkreises für t1=0T, t2=1/8T, t3=1/4T, t4=3/8T und t5=T/2. Gehe dabei auf die
physikalischen Größen ein, welche sich zeitlich periodisch ändern.
• Gib an, was man unter der thomsonschen Schwingungsgleichung versteht.
• Bei der Thomsonschen Schwingungsgleichung geht man vereinfachend von einem idealen
Schwingkreis aus. In der Realität kann aber der ohmische Widerstand nicht vernachlässig
werden. Beschreibe und erkläre dessen Einfluss auf den Verlauf der Schwingung.
Vielen Dank
3 Antworten
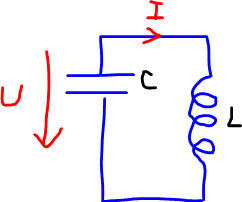
Kondensator uns Spule bilden einen ungedämpften Schwingkreis (siehe Bild). Strom und Spannung folgen einem sinusförmigen Verlauf, sind aber gegenseitig um 90° phasenverschoben.

jetzt muss du nur überlegen, wie dies konkret aussieht - schaffst du es mit diesem Tipp?

https://de.wikipedia.org/wiki/Schwingkreis
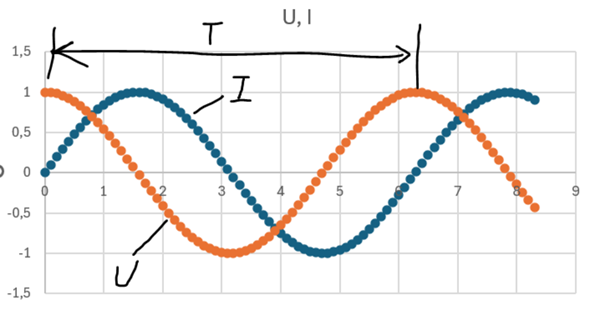
erklärt das recht gut. Dazu muss man wissen, dass im zeitlichen Verkauf (Abb. 3) die Periodendauer T dem Wert 2*Pi entspricht.
Die Thomsonsche Schwingungsgleichung berechnet die Resonanzfrequenz, das ist die Frequenz, mit der der Schwingkreis frei und ungedämpft schwingt.
Das bekommt man durch Lösen der Differentialgleichungen hergeleitet.
Alternativ hilft die komplexe Wechselstromrechnung:
Die Resonanzfrequenz ist bei einem Parallelschwingkreis die Frequenz, bei der dieser Schwingkreis einen unendlich hohen komplexen Widerstand (Impedanz) bzw. den Leitwert (Admittanz) 0 hat. Daraus erhält man die gesuchte Formel. Das ist deutlich einfacher.
Wenn der Schwingkreis durch einen Widerstand gedämpft wird, wird die Amplitude der Schwingung mit der Zeit immer kleiner. Außerdem verringert sich die Resonanzfrequenz.
Wenn die Dämpfung allzu groß wird, tritt der "Kriechfall" ein und der Schwingkreis schwingt überhaupt nicht mehr.
Das bekommt man durch Lösen der Differentialgleichungen hergeleitet.
Noch einfacher: 1/(omega*C) = omega * L
Das wird vielerorts gut erklärt.