Funktion oder keine Funktion?
Hallo liebe Mitmenschen,
Frage steht oben. Meine Unklarheit liegt darin, dass eine Funktion diesen Aufbau hat: y = mx+c, also eine Gerade halt. Aber eine Funktion macht auch aus, das jeder x wert je einen y wert hat, welches hier ja auch der Fall ist. Nur ist diese unten keine Gerade, aber eine Funktion muss doch eine Gerade sein... Also ist dies eine Funktion oder nicht (bitte mit Begründung und Aufklärung)
4 Antworten
Eine Funktion muss doch keine Gerade sein. :)
Eine Gerade ist eine lineare Funktion.
Es gibt aber auch Funktionen mit einem höheren Grad. Quadratische Funktionen, Funktionen 3. Grades, 4. 5. 10. Grades usw.
Es gibt Logarithmusfunktionen, Exponentialfunktionen usw.
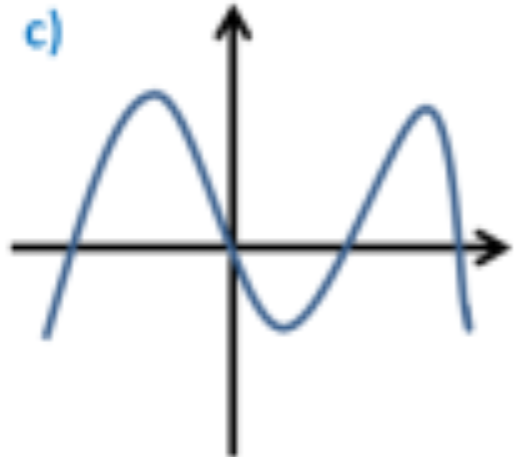
Das in dem Bild ist mindestens eine Funktion 4. Grades, da es mindestens 4 Nullstellen im gezeigten Wertebereich gibt.
Um nochmal genau auf Deine Problematik zurück zukommen, es handelt sich hierbei um ein Polynom 4. Grades:
Ich glaube Du meinst die Nullpunkte, an deren Position ist die Steigung, also die erste Ableitung f(x)´= 0
Die Ableitung einer Geraden ist eine Konstante, wie z.B. 3 oder 5 oder 12 etc...
Betrachten wir im folgenden f: IR -> IR. Wenn f linear ist, dann gilt: Für bel. a,x,y aus IR: f(x+y)=f(x)+f(y) und f(ax)=af(x)
Nein, x ist an diesen Stellen nicht =0 sonder die Ableitung ist Null.
Bei der Nullstellenberechnung wird f(x)=0 gesetzt.
f(x)=0 = mx + b
Du meinst die Nullstellenberechnung mit der X Achse. :)
Beim Einsetzen von x=0 kannst Du aber den Schnittpunkt mit der Y-Achse berechnen.
Aber ich hab einen kleinen Fehler in meinem 1. Post, es handelt sich um eine Funktion 4. Grades, da 4 Nullstellen existieren. :)
für lineare Funktionen gelten die oben genannten Eigenschaften. Danach gilt: f(0)=0*f(0)=0.
Ja das stimmt halt nicht.
F(x=0) ist nicht gleich 0. Das ist soweit ich mich erinnern kann einfach falsch.
Nur im Schnittpunkt mit der Y-Acshe ist x=0.
ich spreche nicht über Stammfunktionen oder der Ableitung von f
Ja sorry, kein Plan wovon Du hier schreibst.
F(0)=0 ist für meine Begriffe der Schnittpunkt mit der Y-Achse. :)
In der Schule bekommt man fälschlicherweise beigebracht, bei Funktionen der Art f(x)=mx+b, handle es sich um lineare Funktionen. Im Mathematikstudium lernt man im 1. Semester lineare Funktionen richtig kennen.
Ich habe Maschinenbau studiert, dort hab ich das so gelernt. :)
Nein, hatte mich eben falsch ausgedrückt und es auch gleich korrigiert.
Aber ich sehe jetzt mal im Papula nach.
Sorry, aber nach Papula ist meine Form richtig.
Hauptform einer Geraden
y=mx+b ; m=tan α bzw. m=(y-y1)/(x-x1)
bzw. m=f(x)´
Wie lautet denn die genaue Bezeichnung von Deiner Version?
Bestimmt haben wir im Maschinenbau das Thema weniger ausführlich bearbeitet als Mathematiker. Aber vielleicht kennt der Papula das auch.
¯\_(ツ)_/¯
https://de.wikipedia.org/wiki/Lineare_Abbildung#Definition
Du kannst dir gerne die Definition einer linearen Funktion anschauen.
Als Vektorraum kannst du dir vereinfacht die Reellen Zahlen vorstellen
Naja Vektorraum hat doch mit einer Geradengleichung nichts zu tun.
Bei einer Nullstellenberechnung fängt man doch nicht mit Vektoren an. :)
Äpfel und Birnen würde ich mal behaupten...
Ein Beispiel für einen Vektorraum ist IR. Als Vektoren werden lediglich die Elemente eines Vektorraums bezeichnet.
Ja aber Vektoren wendest Du an bei z.B. gerichteten Kräften. Das hat nicht mit einem Polynom 4. Grades oder der in der Fragestellung genannten Geradengleichung zu tun. Als Mathematiker sollte Dir das doch eigentlich klar sein.
NEIN !!! Vektoren sind Elemente eines Vektorraums. Ja es gibt den IR^2 und IR^3, aus denen man Vektoren für eben solche Kräfte hernehmen kann. Es gibt aber z.B. auch den Vektorraum aller Polynome mit Grad kleiner gleich 5 oder den Vektorraum der Funktionen. Wichtig ist bei der Definition der Linearität, welche Eigenschaften damit einhergehen: die Homogenität und die Additivität.
Ja das mag ja sein, aber hier handelt es sich um ein stink normales Polynom 4. Grades und einer Geradengleichung. :)
Stimmst du mit zu, dass falls f: IR -> IR linear ist, für beliebige a,x aus IR f(ax)=a*f(x) ist?
Kann ich leider nicht, hab auf die Schnelle nichts dazu in meiner schlauen Papula Formelsammlung gefunden.
Ich wüsste auch nicht wie ich von Vektoren auf die Nullstellenberechnung komme.
Nur ist diese unten keine Gerade, aber eine Funktion muss doch eine Gerade sein.
Eine lineare Funktion ist eine Gerade, aber doch nicht eine Funktion generell.
Aber eine Funktion macht auch aus, das jeder x wert je einen y wert hat
Fast : jeder x-Wert hat h ö c h s t e n s einen y-Wert .
.
hier
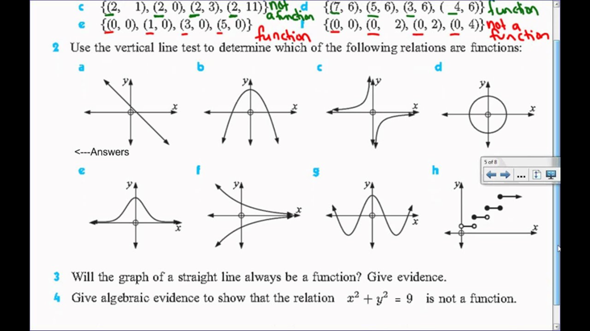
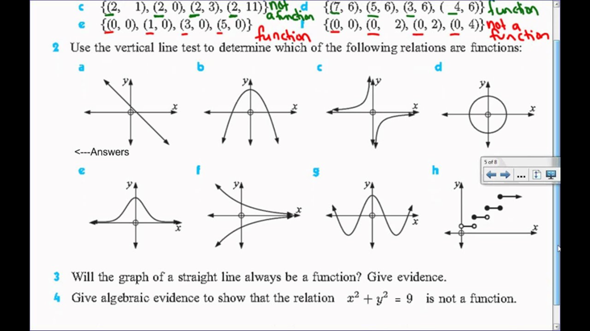
d und f sind keine , alle anderen schon .
bei h) ist durch schwarz weiß gefüllte Punkte sicher gestellt , dass es nicht zwei Werte für ein x gibt : die Enden der Striche ( weiß ) gehören nicht mehr zum Strich , die Anfänge ( schwarz ) jedoch dazu.
Auch das ist eine Funktion. Deine Gleichung beschreibt lediglich eine lineare Funktion. Es gibt noch zig andere Arten mit jeweils charakteristischen Graphen. Einige Funktionstypen nennst du ja schon in den Hashtags.
ok also nur kurz zur Klarstellung, das ist eine Funktion aber keine lineare Funktion, richtig?
Eine lineare Funktion ist immer eine Gerade. Andere Funktionen besitzen jeweils andere Graphen. Also JA
Wenn man ganz genau sein will, ist eine Gerade im allgemeinen keine lineare Funktion, da lineare Funktionen immer 0 auf 0 abbilden (d.h f(0)=0)