Mathe Funktion aufstellen?

Hallo ich habe hier eine Aufgabe, zu welcher ich eine Funktion bilden soll. Es sind Werte gegeben, einpasst von denen helfen die Funktion aufzustellen, andere sind nur zur Irreführung da. Ich finde die passenden Werte nicht, kann wer vielleicht rüberschauen und mir nur die passenden Werte geben? Und wenn meine Werte schon richtig sind, mich verbessern? Wäre sehr hilfreich. Vielen Dank schonmal im Vorraus 🙏🏼

Answer 1

[mihisu]

Du hast da im Grunde nur einen kleinen Vorzeichenfehler gemacht. In der dritten Zeile von unten müsste b = -0,25 statt b = 0,25 stehen. Dementsprechend hast du auch im Ergebnis in der letzten Zeile an einer Stelle ein falsches Vorzeichen.

Richtiges Ergebnis: f(x) = 1/6 x³ - 0,25 x² - 12 x + 1/12

ABER: Du solltest aufpassen, dass du deine Rechnungen nachvollziehbarer aufschreibst! Inbesondere am Ende der 7ten Zeile habe ich länger gebraucht, bis ich nachvollziehen konnte, wie du darauf gekommen bist. [Das stammt nämlich wohl aus der Gleichung der nachvollgenden Zeile. Das ist extremst verwirrend, dass du da etwas, was du aus einer späteren Zeile erhältst in eine vorige Zeile schreibst.] Eine nicht nachvollziehbare Rechnung ist quasi nichts wert! Achte darauf, dass deine Rechnungen für einen Leser nachvollziehbar sind!

===========

Zunächst einmal zur Klärung, welche der angegebenen Gleichungen zur Funktion passt...

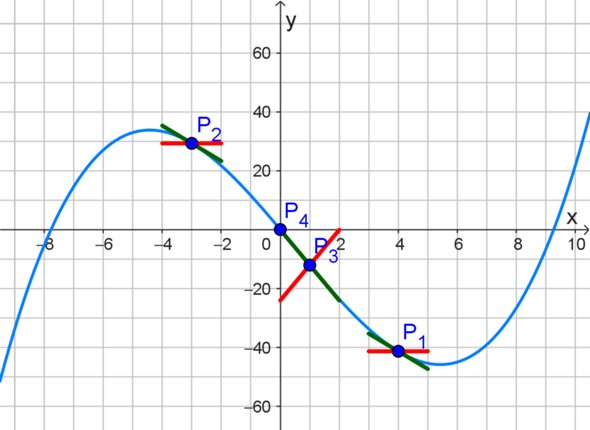
• f(4) = -41,25 passt zur Funktion, da der Punkt P₁( 4 | -41,25 ) auf dem Funktionsgraphen liegt.
• f(-3) = 88/3 [mit 88/3 ≈ 29,33] passt zur Funktion, da der Punkt P₂( -3 | 88/3 ) auf dem Funktionsgraphen liegt.
• f(1) = -12 passt zur Funktion, da der Punkt P₃( 1 | -12 ) auf dem Funktionsgraphen liegt.
• f(0) = 1/12 [mit 1/12 ≈ 0,08] passt zur Funktion, da der Punkt P₄( 0 | 1/12 ) auf dem Funktionsgraphen liegt. [Bemerkung: 1/12 ≈ 0,08 ist hier relativ nah an 0, sodass es so aussieht, als ob der Funktionsgraph durch den Ursprung (0 | 0) verlaufen würde, also f(0) = 0 statt f(0) = 1/12 wäre.]
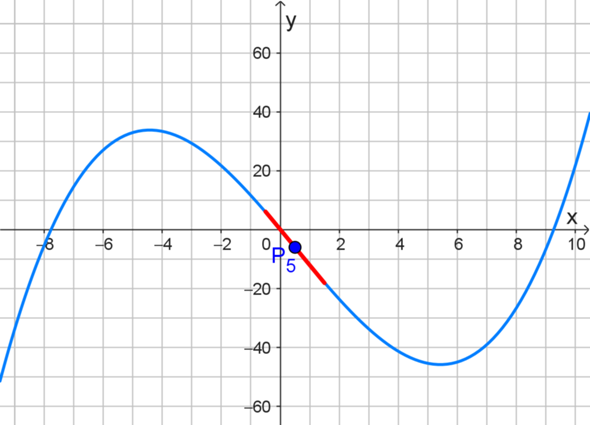
• f′(0,5) = -12,125 passt zur Funktion. Denn an der Stelle x = 0,5 beträgt die Tangentensteigung -12,125. [Siehe: rote Tangenten-Linie um P₅ im zweiten Bild.]
• f′(4) = 0 passt nicht zur Funktion. Denn an der Stelle x = 4 beträgt die Tangentensteigung etwa -6 statt 0. [Siehe: unpassende rote Linie um P₁ im Vergleich zur dunkelgrüne Tangenten-Linie um P₁.]
• f′(-3) = 0 passt nicht zur Funktion. Denn an der Stelle x = -3 beträgt die Tangentensteigung etwa -6 statt 0. [Siehe: unpassende rote Linie um P₂ im Vergleich zur dunkelgrüne Tangenten-Linie um P₂.]
• f′(1) = 12 passt nicht zur Funktion. Denn an der Stelle x = 1 beträgt die Tangentensteigung etwa -12 statt 12. [Siehe: unpassende rote Linie um P₃ im Vergleich zur dunkelgrüne Tangenten-Linie um P₃.]
• f′′(0,5) = 0 passt zur Funktion. Denn an der Stelle x = 0,5 hat die Funktion ihren Wendepunkt (hier: Übergang von Rechtskrümmung zu Linkskrümmung). [Bemerkung: f′′(x₀) = 0 ist bei mindestens zweimal differenzierbaren Funktionen eine notwendige Bedingung für eine Wendestelle bei x = x₀.]

Es sind also 6 von den 9 angegebenen Gleichungen richtig. Für eine ganzrationale Funktion dritten Grades reichen jedoch 4 (voneinander linear unabhängige) Gleichungen aus. Du hast 4 passende Gleichungen ausgewählt. Und du hast auch mit f(x) = ax³ + bx² + cx + d einen passenden Ansatz gewählt. Das, was du da aufgeschrieben hast, ist jedoch erst einmal etwas unübersichtlich. Ich würde das mal versuchen, etwas übersichtlicher aufzuschreiben, um das besser nachzuvollziehen...

$f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+d$

$f'(x)=3\cdot a\cdot x^2+2\cdot b\cdot x+c$

$f''(x)=6\cdot a\cdot x+2\cdot b$

------------------

$\left[\text{A}\right] :\quad f(4)=-41\text{,}25$

$\left[\text{B}\right] :\quad f(1)=-12$

$\left[\text{C}\right] :\quad f(-3)=\frac{88}{3}$

$\left[\text{D}\right] :\quad f''(0\text{,}5)=0$

------------------

$\left[\text{A}2\right] :\quad 64a+16b+4c+d=-41\text{,}25$

$\left[\text{B}2\right] :\quad a+b+c+d=-12$

$\left[\text{C}2\right] :\quad -27a+9b-3c+d=\frac{88}{3}$

$\left[\text{D}2\right] :\quad 3a+2b=0$

------------------

$\left[\text{D}2\right]\rightarrow\left[\text{D}3\right]:\quad b=-1\text{,}5 a$

$\left[\text{D}3\right]\text{ in }\left[\text{C}2\right]\rightarrow\left[\text{C}3\right]:\quad -27a+9\cdot \left(-1\text{,}5a\right)-3c+d=\frac{88}{3}$

$\left[\text{D}3\right]\text{ in }\left[\text{A}2\right]\rightarrow\left[\text{A}3\right]:\quad 64a+16\cdot \left(-1\text{,}5a\right)+4c+d=-41\text{,}25$

$\left[\text{A}3\right]\rightarrow\left[\text{A}4\right]:\quad 40a+4c+d=-41\text{,}25$

---------

$\left[\text{E}\right]:\quad f'(0\text{,}5)=-12\text{,}125$

$\left[\text{E}2\right]:\quad 0\text{,}75 a+b+c=-12\text{,}125$

$\left[\text{D}3\right]\text{ in }\left[\text{E}2\right]\rightarrow\left[\text{E}3\right]:\quad 0\text{,}75 a-1\text{,}5a+c=-12\text{,}125$

$\left[\text{E}3\right]\rightarrow\left[\text{E}4\right]:\quad c=0\text{,}75 a-12\text{,}125$

---------

$\left[\text{E}4\right]\text{ in }\left[\text{A}4\right]\rightarrow\left[\text{A}5\right]:\quad 40a+4\cdot\left(0\text{,}75-12\text{,}125\right)+d=-41\text{,}25$

$\left[\text{A}5\right]\rightarrow\left[\text{A}6\right]:\quad 43a+d=7\text{,}25$

$\left[\text{A}6\right]\rightarrow\left[\text{A}7\right]:\quad d=7\text{,}25-43 a$

---------

$\left[\text{D}3\right],\left[\text{E}4\right],\left[\text{A}7\right]\text{ in }\left[\text{B}2\right]\rightarrow\left[\text{B}3\right]:\quad a-1\text{,}5 a+0\text{,}75a - 12\text{,}125+7\text{,}25-43 a=-12$

$\left[\text{B}3\right]\rightarrow\left[\text{B}4\right]:\quad -42\text{,}75 a=-7\text{,}125$

$\left[\text{B}4\right]\rightarrow\left[\text{B}5\right]:\quad a=\frac{1}{6}$

$\left[\text{B}5\right]\text{ in }\left[\text{D}3\right]\rightarrow\left[\text{D}4\right]:\quad b=-0\text{,}25$

---------

$\left[\text{B}5\right]\text{ in }\left[\text{E}4\right]\rightarrow\left[\text{E}5\right]:\quad c=0\text{,}75\cdot \frac{1}{6} - 12\text{,}125=-12$

$\left[\text{B}5\right]\text{ in }\left[\text{A}7\right]\rightarrow\left[\text{A}8\right]:\quad d=7\text{,}25- 43\cdot \frac{1}{6}=\frac{1}{12}$

Ergebnis:

$f(x)=\frac{1}{6}\,x^3-0\text{,}25\, x^2-12\,x+\frac{1}{12}$

Comments

[KadaverUnruh]

Hey also das mit dem Zeilen Ding is so ne Sache. Und zwar sehe ich es echt gern wenn ich Arbeitsblätter vollschreibe. So das sozusagen keine leeren Lücken mehr vorhanden sind. Ich finde es einfach, naja, schön anzusehen, wie alles relativ ordentlich geschrieben und ausgefüllt ist. Natürlich weiß ich das ich das als Hausaufgaben oder so, so nicht abgeben kann. Das sind eher Übungen für mich. Und das mit der extra Bedingung, ja das hab ich vergessen nachzutragen. Ich weiß nicht mehr wieso aber irgendwie hatte mich die Aufgabe meine Synapsen irgendwie verwurschtelt und ich war einfach ähnlich zu faul alles nochmal aufzuschreiben. Also vielen lieben Dank für diese sehr detaillierte und hilfreiche Erklärung 🙏🏼 ♥️

Answer 2

[gauss58]

(1) f(4) = -41,25

(2) f(1) = -12

(3) f(-3) = 88/3

(4) f'(0,5) = -12,125

Das führt zu:

f(x) = (1/6) * x³ - (1/4) * x² - 12x + (1/12)

f(0) = 1/12 und f''(0,5) = 0 werden bestätigt.

f'(-3) = 0 und f'(4) = 0 und f'(1) = 12 sind falsch.

Comments

[KadaverUnruh]

Oh, danke, war nur dieser kleine Vorzeichenfehler. Vielen Dank fürs aufzeigen 🙏🏼