Flächeninhalt zwischen 2 Graphen?
Hallo,
ich habe in Mathe eine Aufgabe und komme einfach nicht weiter
Aufgabe:
Der Vogelschutzverein VoSchu möchte als Vereins-logo das stilisierte Seitenbild eines Wiedehopfs benutzen. Dabei soll im Intervall [-6; -0,2] der Graph von f mit
f(x) = (-15x - 10) e^3x die obere und der Graph von g mit g(x) = -10e^x die untere Kurve des Bildes darstellen (Längeneinheit cm). Die Federhaube soll bei Berechnungen nicht berücksichtigt werden.
d) Bestimmen Sie den Flächeninhalt des Vereinslogos, wenn das Logo unten durch die Gerade y = f(-0,2) begrenzt wird.

Ich weiß eigentlich wie man eine Fläche zwischen Graphen ausrechnet (Differenzfunktion),doch die Begrenzung durch die Gerade verwirrt mich und ich weiß nicht was ich da machen soll?
lg Wanja
2 Antworten
y=f(-0.2) ist eine waagrechte Gerade, die die Fläche nach unten begrenzt
y ausrechnen
dann den Schnittpunkt mit g ausrechnen g(x)=y und daraus dann x als Intervallgrenze
die Fläche setzt sich aus zwei Teilflächen zusammen
erste Teilfläche im Intervall [-6;x] obere Funktion f, untere g
zweite Teilfäche im Intervall [x,-0.2] obere Funkton f, untere y (waagrechte Gerade)
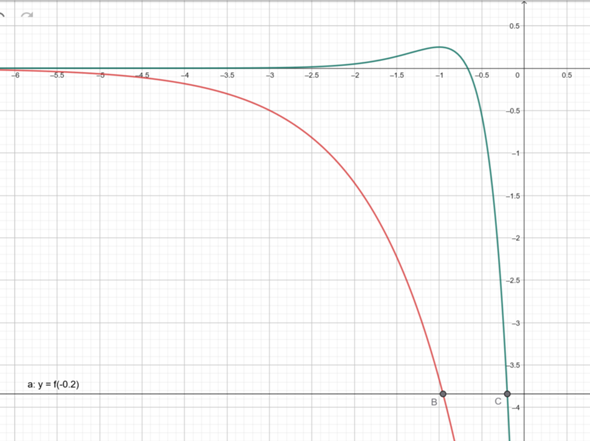
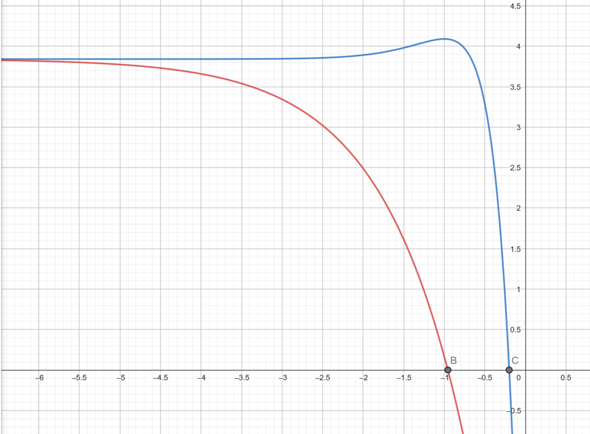
Die Figur sieht folgendermaßen aus:

Der Punkt B ist die Schnittstelle von g(x) mit der Geraden f(-0.2)
g(x) = f(-0.2) für x ~ -0.956675
Der Punkt C ist die Schnittstelle von f(x) mit der Geraden f(-0.2)
f(x) = f(-0.2) für x = -0.2
Außerdem gilt y = f(-0.2) ~ -3.84168
###
Das Integral der Differenzfunktion f(x) - f(0.2) über dem Intervall von -6 bis zum Punkt C: [-6, -0.2] ergibt A1 ~ 21.906125
Das Integral der Differenzfunktion g(x) - f(0.2) über dem Intervall von -6 bis zum Punkt B: [-6, -0.956675] ergibt A2 ~ 15.54309
Gesamtfläche : A = A1 - A2 = 21.90612 - 15.54309 ~ 6.36303
Zur Erklärung : man schiebt beide Funktionen um | f(-0.2) | nach oben und kann dann die untere Fläche von der oberen Fläche unter Berücksichtigung der passenden Intervallgrenzen abziehen. Die Betrachtung der Diferenzfunktion f(x) - g(x) macht wenig Sinn, weil die nur bis zum Punkt B gültig ist.