An welchen Stellen hat g(x) den Anstiegswinkel -40 Grad?
g(x) ist 0,25x hoch 4 - 0,8x hoch 3 + 2x
Ich habe eine Ableitung der Funktion schon gemacht.
x hoch 3 - 2,4x hoch 2 + 2
Komme aber nicht klar, wie man die Stellen bei einem Winkel schriftlich berechnet. Die pq-Formel passt in diesem Fall nicht. Könnte mir jemand es erklären, bitte? Ich lerne für die Klausur und ich will es richtig lösen können
4 Antworten
Ich würde denke ich folgendermaßen da rangehen.
Wenn ich mich recht erinnere gibt mir die erste ableitung ja die Steigung an der stelle x.
prüfen wir das kurz prinzipiell nach:
f(x) = 2x
Erste ableitung ist 2.
Und beid er geraden gehen wir 1 nach rechtes und 2 nach oben.
Gut.
Nun haben wir ja hier ein steigungsreieck. und sie wollen wissen an welchen stellen steigungswinkel -40 grad ist.
Was wir nicht wissen: Welche steigung ist das überhaupt.
Steigusngsdreieck aufzeichnen und schauen was wir haben:
Wir wissen den Winkel. 40 grad (das minus bedeutet hier warscheinlich das es sich um eine fallende steigung handelt)
Die ankathete: 1
Und wir brauchen die gegenkathete: x
Die können wir dann mit dem Tangens berechnen. Tan 40grad = 1/x
Wenn wir unser x haben. Packen wir noch das - ran (bzw nehmen es mal -1 oder berechnen gleich den tanges von -40 grad...) es handelt sich ja um eine negative steigung. Und setzen das gleich deiner ersten ableitung. (ich nehme hier y weil x ja schon vergeben ist. Du hast dann an der stelle ja ne zahl.) Also:
x hoch 3 - 2,4x hoch 2 + 2 = -y
So umformen das du = 0 hast.
Und dann ganz normal die nullstellen einer Funktion 3. grades berechnen. Wie das geht kannste ggf. in deinen schulbüchern nochmal nachlesen. Das müsstest du ggf. schonmal gehabt haben. Ich hatte es nie.
Was aber geht ist diese komische faktoren zerlegung. Also das ausklammern von x das du den term in form von: x * (x+2) * (x+3) oder so hast. Schau mal ob das ggf. geht.
Edit: Das was ich weiter oben mit dem Steigunsgdreieck so schön schlampig hergeleitet habe ist das was cvtldochda in einer zeile gesagt hat.
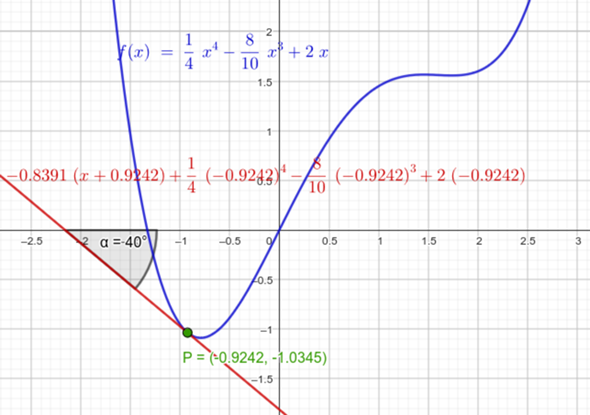
f(x)=¼x⁴−⅘x³+2x
f’(x)=x³−2⅖x²+2
Jetzt willst Du wissen, an welchen Stellen f(x) mit −40° ansteigt, also f’(x)=tan(−40°)≈−0.839099631177. Du suchst also die Lösung der kubischen Gleichung
x³ − 2⅖x² + 2.839099631177 = 0
und diese Gleichung hat nur eine reelle Lösung, nämlich x=−0.92416409109092. Kubische Gleichungen haben ja immer drei Lösungen, diese hat eine reelle und zwei komplexe, die uns nicht weiter interessieren.
Zum Lösen kubischer Gleichungen gibt es ein Kochrezept:

In Deinem Fall hast Du a=−2.4, b=0 und c=2.839099631177. Daraus berechnest Du κ=5.76 und λ=−49.00769004178656. Da λ²>4κ³, hat die Gleichung nur eine reelle Lösung und Du setzt in die erste der drei Lösungsformeln ein. Ehrlich gesagt sehe ich nicht, wie man billiger an die Lösung kommen kann, außer Du willst es numerisch machen, z.B. mit Newton.
Spaßeshalber mache ich jetzt nochmals dasselbe für Tangenten mit Steigungswinkel +40°. Hier muß f’(x)=x³−2⅖x²+2=+0.839099631177 gelten, man bekommt also die kubische Gleichung
x³ − 2⅖x² + 1.1609003688227 = 0
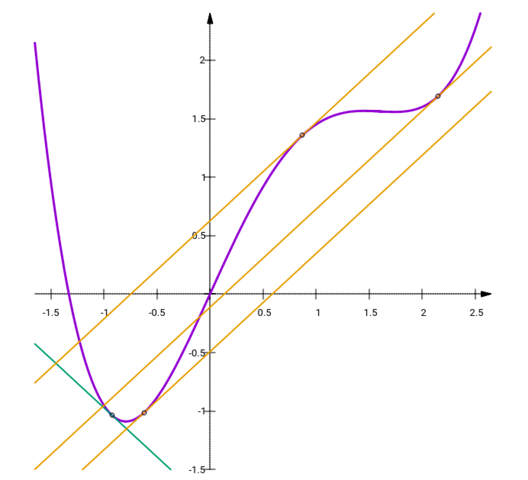
und wir berechnen wieder κ=5.76 und λ=−3.69630995821. Da aber in diesem Fall λ²<4κ³, hat die Gleichung drei reelle Lösungen und Du setzt in die zweite der drei Lösungsformeln ein; Du bekommst die drei x-Werte −0.620002995, 0.8714925943 und 2.1485104011. Das sind also die x-Werte, an denen die Funktion mit +40° ansteigt, und hier sieht man das alles geplottet:

Die violette Kurve ist die Funktion, die grüne Tangente ist die von Dir gesuchte mit Steigungswinkel −40°, und die drei gelben Tangenten sind die von mir spaßhalber dazugerechneten mit +40°. Du siehst ganz anschaulich, daß es wirklich einmal nur eine gibt und das andere Mal drei davon.

Es gilt:
Also musst Du diese Gleichung lösen.
Anmerkung: Ohne Hilfsmittel wird das nicht funktionieren.
Skizze:

" g(x) ist 0,25x hoch 4 - 0,8x hoch 3 + 2x "
Es wäre sehr hilfreich, wenn du den Funktionsterm in klar verständlicher Weise (entweder durch graphische Formeldarstellung oder aber mit ausreichenden und korrekt gesetzten Klammern) so angeben würdest, dass man ihn auch richtig verstehen kann !
-------------------------------------------------------------------------
... und ferner:
"An welchen Stellen hat g(x) den Anstiegswinkel -40 Grad?"
g(x) ist nur ein Funktionsterm und keine Kurve und hat deshalb überhaupt keine "Anstiegswinkel" !