Wie schreibe ich eine Funktion welche eine absteigende Diagonale zeichnet?
Hallo!
Ich soll für einen Canvas eine Funktion schreiben, wo der ersten Pixel der ersten Reihe oben links schwarz gefärbt werden soll, dann in der zweiten Reihen die ersten zwei, in der dritten die ersten drei und so weiter bis zum Ende des Canvas. Der Canvas ist 200x200 Pixel groß.
Ich weiß das die Position Links obere Ecke diese Position ist: (0, height - 1), rechts obere Ecke: (width - 1, height - 1)links untere: (0, 0) und rechts untere (width -1, 0).
Wenn ich also c = canvas_set_black(c, 0, 0); durchführe, würde das den Pixel der linken untere Ecke Schwarz färben.
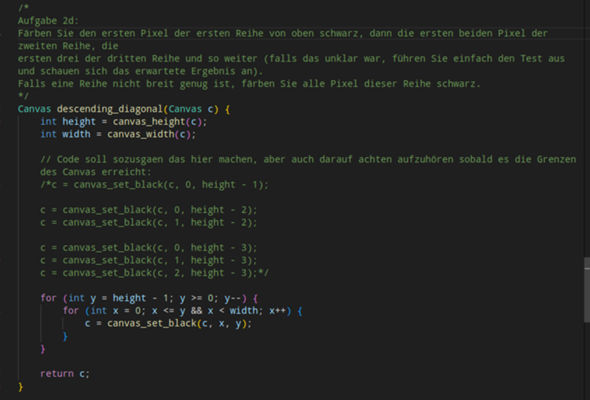
Auf jeden Fall macht mein Code ungefähr was er soll, aber nicht an der richtigen Position. Hier mein Code (Bild 1) und das Ergebnis (Bild 2). Im zweiten 2 ist das obere Bild das Ergebnis meines Canvas und das untere Bild, das erwartete Ergebnis des Canvas. Wie man sehen kann färbt es zwar eine absteigende Diagonale, aber nicht an der Ecke die ich eigentlich möchte. Irgendeinen Tipp?