Was muss man bei e) machen? Reicht es wenn man zeigt wie man auf die erste Ableitung kommt?

3 Antworten
Was muss man bei e) machen? Reicht es wenn man zeigt wie man auf die erste Ableitung kommt?
Nein, das reicht nicht, denn es ist explizit nach D, also dessen Koordinaten gefragt. Die müssten lauten:
Dazu muss man zuerst die Abstandsfunktion aufstellen (ziemlich schwierig), diese Ableiten und die Ableitung zu 0 setzen. Damit hat man den x-Wert von D und über die Funktion des Verbindungsweges kriegt man auch den y-Wert raus.
m.E müsste rauskommen: D(2,606 / -0,099)
Danke, ich versuche mich weiter an diese Aufgabe.a) bis d) waren einfach bloß e) ist halt sehr schwierig.
Ich hab mir die Aufgabe mal angeschaut und ich muss ehrlich sagen, dass ich die Frage nach dem "weitesten Abstand zum südlichen Rand" anders verstanden hätte, wie es hier getan wurde, aber der gesuchte Rechenweg ist offensichtlich wiefolgt:
Zuerst einmal muss man sich klar machen, dass f(x) nicht nur durch Punkt P, sondern auch Punkt N geht.
Da der Weg von P nach N (es ist offensichtlich ein geradliniger Weg gemeint, auch wenn das genau genommen nicht im Text steht) schneidet die Funktion f also in genau diesen beiden Punkten, d.h. der Abstand zum Wald ist in P und N gleich Null.
Der Waldrand hat eine ganz leichte Krümmung, sodass der Weg sich kaum vom Wald entfernt:

Hier kommt jetzt der Punkt, an dem ich den Text anders ausgelegt hätte.
Der Begriff "Abstand" impliziert für mich die kürzestmögliche Distanz von einem Punkt zu einem anderen Objekt. Wenn man z.B. genau in der Mitte von P und N stehen würde, dann wäre der Abstand zu P oder N ganz offensichtlich viel länger als zu den Bäumen, die nur wenige Meter entfernt sind.
Daher würde ich denken, dass der Abstand als kürzestmögliche Distanz verstanden werden sollte, d.h. so, dass die Verbindung von dem gewählten Punkt zum gewählten Objekt (hier: der Waldrand) in einem rechten Winkel auftritt.
An jedem Punkt des Weges zwischen P und N gäbe es also einen kürzestmöglichen Abstand zur Funktion f, die den südlichen Waldrand darstellt, und von diesen Abständen würde man dann wiederum den längsten suchen.
So ist das hier aber anscheinend nicht gemeint.
Wie hier gerechnet wurde, ist dass man die Entfernung an einem Standort des Weges zu dem Teil des Waldrands misst, der sich in exakt nörlicher Richtung befinden, d.h. die Differenz der y-Werte von f(x) und der Weggeraden.
Die Abstandsfunktion ist demnach einfach die Differenz dieser beiden Funktionen.
Die Funktion f ist bekannt.
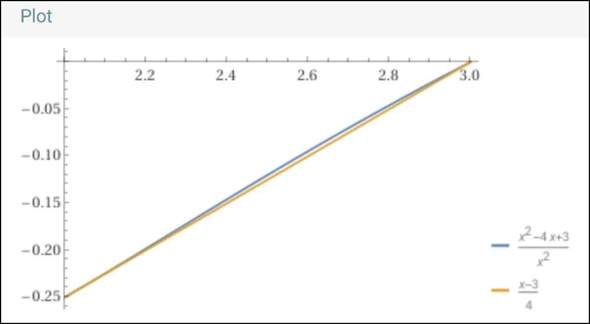
Die Weggerade lässt sich einfach aus den beiden gegebenen Koordinaten als ¼⋅x-¾ ermitteln.
So ergibt sich die Abstandsfunktion:
Die Ableitung dieser Abstandsfunktion ist:
Das lässt sich (fast) zu der im Text gegebenen Ableitung umformen.
Der einzige Unterschied ist ein Vorzeichen.
Das kommt daher, dass die Aufgabensteller die Abstandsfunktion offensichtlich so berechnet haben, dass sie von der Weggeraden die Funktion f abgezogen haben (und nicht umgekehrt).
Das ist in meinen Augen eine schlechte Wahl, denn dadurch ergeben sich auf der ganzen Weglänge negative Abstände.
Wie dem auch sei, so wurde offensichtlich vorgegangen.
Die Extremwerte der Abstandsfunktion lassen sich relativ einfach mithilfe der faktorisierten Darstellung der Ableitung ermitteln. Wir suchen Nullstellen der Ableitung. Eine Nullstelle ist bei x=2. Die anderen beiden ergeben sich aus der zweiten Klammer: x²+2x-12=0 → x₂ = -1+√13 ; x₂ = -1-√13
Die gesuchte Nullstelle muss natürlich zwischen 2 und 3 liegen und das trifft auf -1+√13 zu.
Die zugehörige y-Koordinate auf der Weggeraden ergibt sich mit ¼√13 - 1.
Gerundet sind das die Werte, die auch schon Hamburger02 genannt hat.
Du hast 2 Punkte gegeben, die mit einem Weg verbunden sind. Nämlich ein Weg von P (2/f(2)) nach N (3/0). Auf diesem Weg sollst du jetzt einen Punkt Q finden, der den minimalsten Abstand zum südlichsten Punkt des Parks hat.
Den südlichste Punkt des Parks hast du bereits berechnet. Das ist logischerweise der Tiefpunkt von g(x). Nennen wir ihn S.
Im Hinweis geht es um eine Abstandsfunktion, d.h. du sollst eine Funktion aufstellen, die den Abstand zwischen Q und S beschreibt. Heißt wie groß ist der Abstand zwischen einem allgemeinen Punkt auf deiner Gerade durch P und N, zu dem festen Punkt S.
Wenn du diese Abstandsfunktion aufgestellt hast, willst du natürlich deinen Tiefpunkt herausfinden, da wir den kürzesten Weg suchen. Um den zu berechnen, benötigst du die Ableitung, die eben in der Aufgabenbeschreibung bewiesen werden soll.
Heißt wie groß ist der Abstand zwischen einem allgemeinen Punkt auf deiner Gerade durch P und N, zu dem festen Punkt S.
Da hast du die Aufgabe nicht genau gelesen: es ist nicht der Abstand zum südlichsten Punkt, sondern zum südlichen Rand gefragt und der Rand ist die Funktion f(x). Genau das macht die Aufgabe aber ziemlich kompliziert, denn zunächst muss man die Abstandsfunktion zwischen dem Weg und f(x) aufstellen und das ist beileibe nicht trivial.