Nullstellen gerader und ungerader Ordnung?
Nullstellen von Funktionen mit ungeraden Potenzen haben ja keinen VZW an x0 und andersrum ist es bei geraden Potenzen, das betrifft denke ich mal nur Extremstellen die gleichzeitig auch nullstellen sind?
Meine Frage ist, welchen Anwendungsbezug könnte es in einer Aufgabe geben, sodass einem diese Erkenntnis was bringt
1 Antwort
bei geraden Potenzen von Nullstellen (bei ganzrationalen Funktionen) liegt ein Berührpunkt mit der x-Achse vor, das Schaubild hat dort eine waagrechte Tangente und somit einen Extrempunkt.
bei einer dreifachen Nullstelle hat man auch eine waagrechte Tangente aber mit Vorzeichenwechsel. Das Schaubild hat dort einen Sattelpunkt
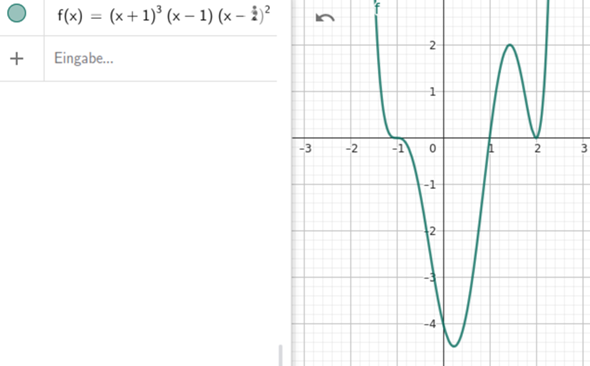
Beispiel:
dreifache Nullstelle bei x=-1 also Sattelpunkt
einfache Nullstelle bei x=1 also "normale" Nullstelle mit Vorzeichenwechsel
doppelte Nullstelle bei x=2 also Extrempunkt mit waagrechter Tangente, kein VZW