Graph Ableitungsfunktion zeichnen?
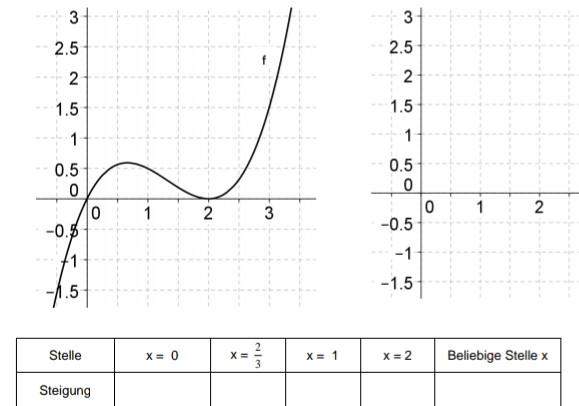
Ich muss von der Funktion einen Graphen der Ableitungsfunktion zeichnen. Wo ist die Steigung, Extremstellen, Nullstellen und Wendepunkt?
4 Antworten
bei x = 0 ist die St eigung positiv
.
bei x = 2/3 gleich Null
danach wird sie negativ
.
bei x = 1 (Wendepunkt) ist die Steigung am kleinsten ( hoher negativer Wert
.
bei x = 2 ist sie wieder gleich Null , danach wird sie wieder positiv
.
Die Ableitungsfkt hat die Form einer nach oben geöffneten Parabel mit den Nullstellen bei 2/3 und 2 und dem Scheitelpunkt bei 1
Leg an den gesuchten Stellen einen Bleistift als Tangete an den Graphen. Dann die Steigung über ein gedachtes Steigungsdreieck abschätzen.
Ist die Funktion bei dieser Aufgabe als Term angegeben, oder muss man die selber herausfinden, oder geht es nur darum, qualitativ die Ableitung zu zeichnen, ohne exakt zu sein?
Oh mann... wusste ich es doch!
f(x) = 0.5x^3 - 2x^2 + 2x
f'(x) = 1.5x^2 - 4x + 2
f'(0) = 2
f'(2/3) = 0 (lokales Maximum)
f'(1) = -0.5
f'(2) = 0 (lokales Minium)
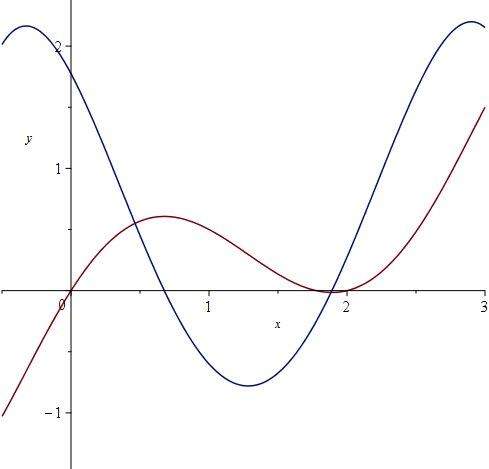
So hier ein Plot.
Braune Kurve ist die Originalfunktion.
Blaue Kurve ist die Ableitung davon.
Somit kannst Du alle Fragen der Aufgabe beantworten.
Ist natürlich nur Qualitativ. Denn die Originalfunktion ist nicht bekannt.
Sorry, die Funktionsgleichung habe ich ausversehen rausgeschnitten die ist: f(x) = 0,5x hoch3 - 2x hoch2 + 2x
Die Aufagbe ist dann den Graphen 'f der Ableitungsfunktion möglichst exakt einzuzeichnen