Wie bestimme ich eine ganzrationale Funktion möglichst niedrigen Grades?
A) S(0/3) ist ein Sattelpunkt des Graphen. Im Punkt P(3/0) liegt eine horizontale Tangente vor.
B) T(2/4) ist Tiefpunkt und W (0/0) Wendepunkt des Graphen. Die Wendetangente hat die Steigung 1.
C) H(0/0) ist Hochpunkt des Graphen. Bei 3 ist eine relative Extremstelle. W(1/11) ist Wendepunkt.
3 Antworten
Hey Jennifer,
das ist einfacher als es zunächst aussieht. Ich rechne Dir die Teilaufgabe A) mal vor, die anderen Aufgaben funktionieren allesamt sehr ähnlich.
A) Es existiert ein Sattelpunkt und ein Extrempunkt (horizontale Tangente).
Für den Sattelpunkt muss die erste Ableitung mindestens zwei Nullstellen haben (sodass die zweite Ableitung eine Nullstelle hat). Für einen Extrempunkt muss die erste Ableitung mindestens eine Nullstelle haben.
Da Extrempunkt und Sattelpunkt aber nicht aufeinander liegen, muss die erste Ableitung mindestens drei Nullstellen haben (eine doppelte für den Sattelpunkt, eine einfache für den Extrempunkt).
Ergo ist die Ausgangsfunktion vom Grad 4.
- f(x) = ax⁴ + bx³ + cx² + dx + e
- f'(x) = 4ax³ + 3bx² + 2cx + d
- f''(x) = 12ax² + 6bx + 2c
- f'''(x) = 24ax + 6b
Sattelpunkt bei (0 | 3):
- f(0) = 3
→ e = 3 - f'(0) = 0
→ d = 0 - f''(0) = 0
→ c = 0 - f'''(0) ≠ 0
→ b ≠ 0
Extrempunkt bei (3 | 0):
- f(3) = 0
→ 81a + 27b + 9c + 3d + e = 0 - f'(3) = 0
→ 108a + 27b + 18c + d = 0 - f''(3) ≠ 0
→ 72a + 6b ≠ 0
Fassen wir also alle Gleichungen nochmal zusammen:
- e = 3
- d = 0
- c = 0
- 81a + 27b + 9c + 3d + e = 0
- 108a + 27b + 18c + d = 0
Aus 1., 2. und 3 folgt:
- 108a + 27b = 0 ⇔ b = -4a
- 81a + 27b + 3 = 0 ⇔ 81a + 27b = -3
Damit haben wir ein lineares Gleichungssystem, das wir ganz einfach durch Einsetzen lösen können.
Wir kommen auf: a = 1/9, b = -4/9
Somit ist unsere Ausgangsgleichung folgende:
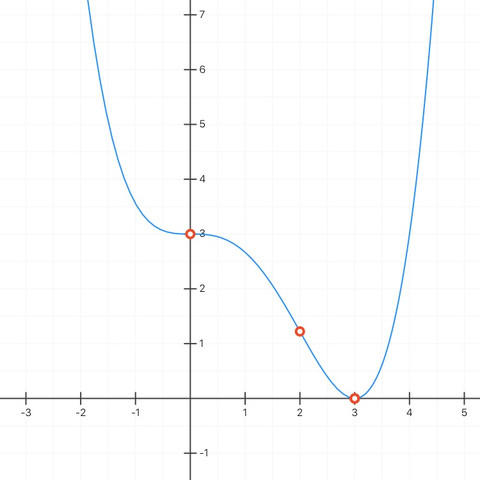
f(x) = 1/9 x⁴ - 4/9 x³ + 3
Ich habe Dir noch ein Schaubild des Graphen angehängt, an dem Du erkennen kannst, wie der Graph verläuft.
——————————————————————
Und genauso machst Du es nun auch bei den anderen Teilaufgaben. Zuerst guckst Du, von welchem Grad das Polynom sein muss und dann stellst Du Gleichungen auf, die dieses beschreiben.
Du solltest dann ein lineares Gleichungssystem erhalten, das Du mithilfe eines bestimmten Lösungsverfahren lösen kannst.
LG Willibergi
Ich hoffe, ich interpretiere es richtig:
Unter Grad 2 geht gar nichts.
Du bekommst dann völlig andere Bilder (Geraden, Hyperbeln).
Ohne Bild, eindeutige Lösung:
f(x) = a (a reelle Zahl)