Nullstellen e Funktion?

moin

Wenn ich

1. (5e^2x)+ (e^-x )

2. E^x+4x²

Habe, wie berechne ich dann Nullstellen/ Extrempunkte?

Ich weiß, wie es bei Kombinationen aus E funktion mal Ganzrationale geht, aber hierbei?

Answer 1

[indiachinacook]

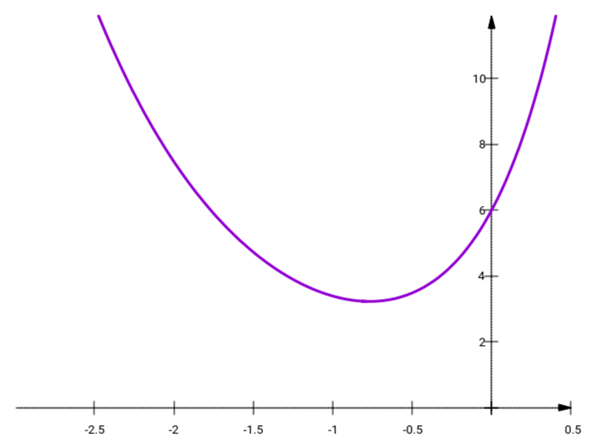
Für die erste Aufgabe ist das ganz einfach: Du siehst auf den ersten Blick, daß zwei Exponetial-Ausdrücke zusammenaddiert werden. eⁱʳᵍᵉⁿᵈᵉᵗʷᵃˢ ist aber immer größer als Null (sofern das irgendetwas reell ist), also gibt es keine Nullstelle.

Für die Extremwerte mußt Du die erste Ableitung Null setzten. Die ist 10e²ˣ−e¯ˣ, und das Nullsetzen geht ganz einfach durch Logarithmieren:

10e²ˣ = e¯ˣ

ln(10)+2x = −x

x = −ln(10)/3 ≈ −0.77

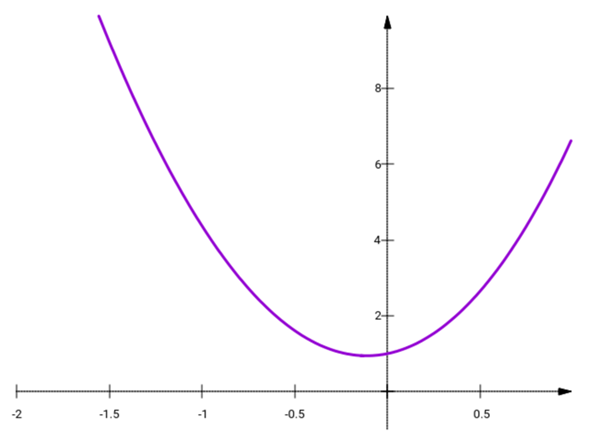
Für die zweite Aufgabe sollen wir den etwas schwierigeren Ausdruck eˣ+4x² her­neh­men. Eine Nullstelle kann es aus demselben Grund wie zuvor nicht geben (beide Sum­manden sind immer positiv), und bei der Ableitung bekommt man eˣ+8x, das hat tat­sächlich eine Nullstelle für ein negatives x:

eˣ = −8x

ln(eˣ) = x = ln(8) + ln(−x)

Wie man diese Gleichung löst, weiß ich nicht, aber ein bißchen numerisches Herumgefummel liefert x≈−0.11178

Woher ich das weiß: Studium / Ausbildung – Chemiestudium mit Diss über Quanten­chemie und Thermodynamik

Comments

[Kelec]

Ausdrücke der Form e^x/x=a lassen sich mit der lambertschen W Funktion lösen:

x=-W(-1/a)

Also in dem Fall

x=-W(1/8)

Soweit mir bekannt ist lässt sich die W Funktion aber nur nummerisch lösen und nur für einige bestimmte Fälle analytisch.

Answer 2

[DerRoll]

Du hast Terme hin geschrieben, keine Funktionen. Ich gehe davon aus dass du die jeweiligen Funktionen

$f(x) = 5*e^{2x} + e^{-x} \text{ und } g(x) = e^x + 4x^2$ meinst. Das funktioniert genau wie bei ganzrationalen Funktionen auch. Ableiten und Nullstellen suchen.