Globales Maximum/ Minimum. Wenn ich u = 2 für A(u) einsetze kommt ein Falsches Erlebnis als es in der Koordinatenachse zeigt?


2 Antworten
Mir scheint, dass die Angabe fehlerhaft ist.
Der Flächeninhalt eines Rechteckts berechnet sich aus Breite mal Höhe.
Da sowohl die Punkte R und P von u abhängen, kann nur der Punkt B (3|0) als fix angenommen werden.
Die Höhe des Rechtecks ergibt sich aus v = A(u) = 7⁄16 u² + 2. Das stimmt noch mit der Aussage in Teilaufgabe a) überein, außer, dass dort unverständlicherweise x verwendet wird und nicht u. Aber die Breite des Rechtecks ergibt sich aus der Differenz der x-Werte der Koordinaten B und R, d.h. 3 und u.
A(u) ist daher (3-u)(7⁄16 u² + 2) und nicht (4-u)(7⁄16 u² + 2).
Wenn wirklich gelten soll u ∈ [0;4], dann haben wir rechnerisch das Problem, dass der Flächeninhalt für u>3 negativ werden, weil die Breite dann negativ wird.
Wir müssen daher den Term |3-u| (7⁄16 u² + 2) maximieren, oder alternativ den größten Betrag des Produktes (3-u)(7⁄16 u² + 2) ermitteln.
Wenn wir Extrema dieser kubischen Funktion ermitteln wollen, dann sehen wir, dass die Ableitung* von A(u) = (3-u)(7⁄16 u² + 2) = -7⁄16 u³ + 21⁄16 u² - 2u + 6 keine Nullstellen hat.
Daraus folgt, dass die Funktion A(u) stetig fällt.
Da wir aber wie gesagt, den Betrag dieser Funktion betrachten müssen, ist entweder der Wert am unteren Definitionsbereich (d.h. u=0) oder am oberen Definitionsbereich (d.h. u=4) der größere.
Setzen wir die Werte also einfach in A(u) ein. A(0) = 3 ⋅ 2 = 6. A(4) = -9, d.h. |A(4)| = 9.
Somit wäre das Rechteck, das mit u=4 gebildet wird, das flächenmäßig größte.
* d A(u) / du = -21⁄16 u² + 21⁄8 u - 2 → diese Funktion hat keine reellen Nullstellen

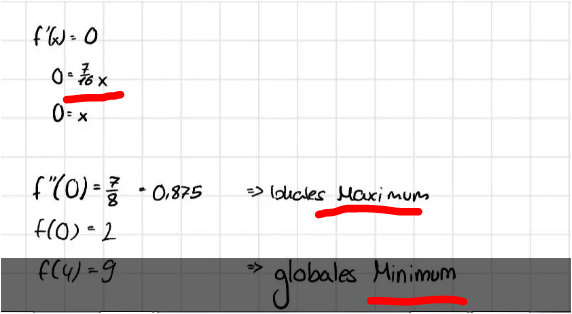
FEhler :
7/8 x = f'(x)
0.875 > 0 ... Minimum
f(4) = 9 , wirklich Minimum ?
Ich meine, wenn ich z.B. 4 in die Flächinhaltsformel einsetze kommt doch 0 raus, wegen (4-4)*(Formel). Macht es dann Sinn wenn die Lage von Q am globalen Maximum liegt?