Wann globale Extrema?
Wie finde ich heraus wenn ein Minimum oder Maximum ein globales Extrema sind? Also wenn ich Minimum und Maximum anhand einer Funktionsgleichung berechnet habe
3 Antworten
Solche Sachen spielen häufig in Anwenden eine Rolle. Ich nehme mal eine Zeichnung aus einem anderen Zusammenhang:
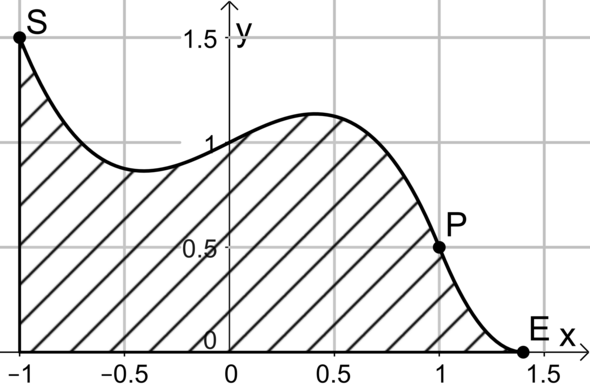
Der Def.-Bereich ist auf das Intervall [-1; 1,4] beschränkt. Gesucht ist das absolute Maximum.
Mit den üblichen Rechenverfahren bestimmt man relative Extrema, also Punkte, die in Relation zu (direkt) umliegenden hoch oder tief liegen. Hier würdest Du als Maximumstelle x = 0,4 (oder so ähnlich) herausbekommen. Hier loegt aber nicht der höchste Wert; der ist bei x = 0. Daher stellt man bei der Suche nach absoluten Extrema immer einen sog. Randwertvergleich an: der maximale relative Funktionswert wird mit den Funktionswerten an den beiden Rändern des Def.-Bereiches verglichen.
Ebenso immer beliebt (in Mathe- und Abiaufgaben): wo ist die Stelle mit der höchsten Steigung? Die ist hier möglicherweise im Wendepunkt P, evtl. aber doch im Startpunkt S.
Das kommt auf die Art der Funktion an.
Bei ganzrationalen Funktionen z. B. gibt es
höchstens n-1 Extrema, wenn n der Grad
der Funktion ist. Die kannst du ermitteln
und schauen, welche den größten/kleinsten
x-Wert hat. Andere gibt es nicht.
Überprüfen welches Maximum/Minimum am größten/kleinsten ist.