Warum ist die Abpumpzeit in einem Vakuumsystem Temperaturabhängig?
Angenommen wir haben ein großes Vakuumystem mit mehreren Komponenten, Ventilen und Rohren im 100mm Durchmesser, dazu eine große Prozesskammer mit einer entsprechend dimensionierten Pumpe. Die Rohrleitungen sind mit Heizdecken umschlossen, die Prozesskammer wird durch einen Thermoreaktor beheizt.
Im kalten Zustand (Raumtemperatur) braucht die Pumpe über einen Bypass 45 Minuten, um den Systemdruck von 750 Torr auf 1.5 Torr zu senken. Ab da wird der volle Rohrquerschnitt freigegeben, sodass die Prozessdruck von 5mTorr erreicht wird.
Im heissen Zustand (Heizdecken um die Vakuumleitungen auf 180°C, große Prozesskammer bei 700°C) braucht sie nur 25 Minuten. Wie lässt sich das physikalisch erklären?
Hat das was mit dem Volumen der im System befindlichen Luft zu tun? Die Leckrate in dem System bleibt gleich.
Liebe Grüße
4 Antworten
Die Formel zur Dichte eines idealen Gases ist:
ρ = p⋅M/(R⋅T)
Bei 700 °C (973,15 K) beträgt diese:
ρ ≈ 0,36 kg/m³
Bei Umgebungsbedingungen beträgt die Luftdichte 1,2041 kg/m³ (20 °C). Somit müssen bei 700 °C nur etwa 30 % der Luftmoleküle entfernt werden, die bei 20 °C abzupumpen sind.
Heiße Luft dehnt sich aus. Folgedessen ist bei gleichen Volumen und höherer Temperatur "weniger" Luft vorhanden. Sie ist nicht so komprimiert.
Es ist einfach Erklärt.
Geht man physikalisch mehr in die Tiefe, sind auch Srömungsgeschwindigkeiten und Reibungsverluste bei Unterschiedlichen Temperaturen noch zu berücksichtigen.
Ein Unterdruck zieht das Gas ja nicht an. Der Druck des Gases selber sorgt dafür, dass sich das Gas in die Richtung wo weniger Druck herrscht bewegt.
Erhitzt man das Gas, erhöht man auch den Druck des Gases bei gleicher Masse. Die Teilchen aus dem das Gas besteht prallen ja ständig aufeinander und prallen voneinander ab. Und die Kraft mit der das passiert hängt von der Temperatur ab. Also gleichen sich Druckunterschiede im System schneller aus wenn das Gas eine höhere Temperatur hat.
Ist der Druck extrem niedrig, also weit unterhalb von dem was auf der Erdoberfläche natürlich vorkommt, dann gibt es einen weiteren Effekt. Die Gasteilchen bewegen sich über weite Strecken ohne gegen ein anderes Teilchen zu prallen. Bewegt sich ein Teilchen von der Pumpe weg, dauert es sehr lange bis es irgendwo an stößt und seine Richtung ändert. Und es braucht im Durchschnitt viele Kollisionen bis sich das Teilchen in Richtung Pumpe bewegt und entfernt werden kann.
Und je heißer das Gas, desto schneller sind die Teilchen unterwegs und je kürzer die Zeit bis es irgendwo kollidiert. Das reduziert dann die Zeit die es dauert bis es zufällig die Pumpe trifft.
Das ist auch der Grund warum man ein Hochvakuum mindestens zweistufig herstellt. Einersetzs hat das mit der Bauweise der verschiedenen Pumpen zu tun, andererseits ob das Gas physikalisch eine Flüssigkeit ist oder man das als einzelne Teilchen die fast gar nicht mehr interagieren auffassen kann.
Wir haben in der Prozesskammer und im Rohrsystem ein bestimmtes Volumen an Luft V_o. Diesem Luftvolumen entpricht eine bestimmte Stoffmenge, die man über die Zustandsvariablen und das ideale Gasgesetz ausrechnen kann.
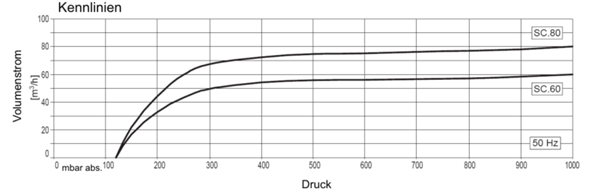
Diese Umrechnung benötigen wir, da die Hersteller von Vakuumpumpen die Pumpleistung ihrer Pumpen immer in Volumentsrom bezogen auf den Zustand am Eintritt der Pumpe angeben. Diese Werte stellen sie in einer Pumpenkennlinie dar, die beispielsweise so aussieht:

Alle handelsüblichen Vorvakuumpumpen, die in der Regel ein- oder zweisufige Drehschieberpumpen sind (seltener Rootspumpen oder Schraubenspindelpumpen) haben qualitativ ähnliche Kennlinien, die bauartbedingt sind.
Egal bei welchem Zustand sich das Gas befindet, können wir aber feststellen, dass bei gleichem Zusand des Gases immer gilt:
Volumenstrom ist proportional zum Stodffstrom, den wir in mol pro Stunde ausdrücken können.
Die Aufgabe der Pumpe besteht darin, eine gewisse Stoffmenge Luft (mol) aus der Aparatur abzupumpen. Je höher der Volumenstrom, umso höher auch der Stoffstrom und je höher der Stoffstrom, umso schneller ist der Apparat leer und der Druck auf den gewünschten Wert abgesunken.
Nun schauen wir uns die Pumpenkennlinie nochmal genauer an: die verläuft am Anfang des Pumpvorganges (rechter Zweig) . Was wir erkennen können: je höher der Druck, umso größer der Volumenstrom und damit auch der Stoffstrom.
Genau das passiert, wenn wir die Appartur erwärmen. Der Druck steigt. Bei konstanten Volumen (der Apparat bleibt ja gleich groß) können wir das Gesetz von Amntons anwenden, welches aus der idealen Gasgleichung hergeleitet ist:
Bei einer isochoren Erwärmung gilt für ideale Gase:
p/T = const.
Draus folgt:
p2 = p1 * T2/T1
Das Verhältnis T2/T1 gibt das Verhältnis des Druckanstieges an. Das rechnen wir mal für die Prozesskammer aus:
T2/t1 = 973/293 = 3,3
Der Druck im System steigt also auf das 3,3 fache. Daraus folgt, dass durch diesen Druckanstieg, der sich über den gesamten Pumpvorgang erstreckt, der Stoffstrom deutlich erhöht wird.
Was wir an der Pumpenkennlinie ebenfalls erkennen (mehr links): ab etwa 300 mbar (230 Torr) nimmt der Volumen-/Stoffstrom stark ab. Durch die Erwärmung und die damit verbundene Druckerhöhung können wir diesen Punkt aber weit hinauszögern, sodass durch die Erwärmung länger mit hohem Stoffstrom abgepumpt wird als bei Zimmertemperatur.