Mantelfläche und Volumen von Rotationskörpern?
Um das Volumen von Rotationskörpern zu berechnen, kann der Körper einfach in unendlich viele infinitesimal kleine Zylinder mit dem jeweiligen Volumen von pi*r^2*h aufgeteilt werden, daraus folgt V=pi*Integral_a^b{(f(x))^2}dx (der Formel-Editor funktioniert nicht).
Warum kann man das bei der Mantelfläche nicht auch mit unendlich vielen infinitesimal kleinen Zylinderwänden machen, mit der Fläche von je 2*pi*r, also A_M=2*pi*Integral_a^b{f(x)}dx?
Und wieso funktioniert es dann mit der infinitesimal kleinen Bogenlänge? Bzw. warum braucht man die dann nicht auch zur Berechnung von dem Volumen? Und wie soll man damit dann exakt die infinitesimal kleine Fläche berechnen können? Wenn man z.B. eine Mantelfläche von einem Kegel ausrollen täte, wäre die ja auch nicht gleich dem Radius der Grundfläche mal der Länge der Seitenkante?
3 Antworten
Die Mantelfläche eines Rotationskörpers f(x) im Intervall [a, b] wird nicht über Zylinder bestimmt, sondern über Kegelstümpfe.
Die Mantelfläche eines Kegelstumpfs beträgt:
M = (r1 + r2) * π * m
m ist dabei die Länge der Seitenkante von Radius r1 bis r2.
Teilt man die Höhe des Rotationskörpers in infinitesimale Kegelstümpfe, dann gilt
Das Rotationsintegral für die Mantelfläche lautet deshalb:
Beispiel Kegel mit r = 1 und h = 1:
f(x) = 1 - x, a = 0, b = 1
###
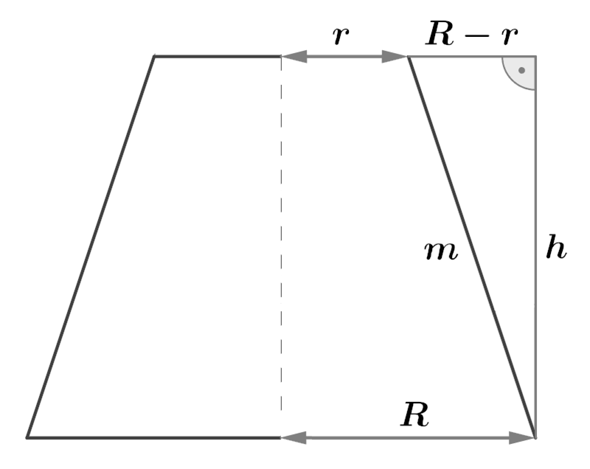
Warum für die Mantelfläche eines Kegelstumpfs
M = (R + r) * π * m
gilt, lässt sich am folgendem Bild erklären:

- m ist die Breite des Kegelstumpfs (Phytagoras), m = sqrt( (R-r)² + h²)
- der mittelere Radius des Kegelstumpfs beträgt (R+r)/2
- der mittlere Umfang dann U = 2*π*(R+r)/2
Die Mantelfläche ist dann Breite * Umfang:
M = m * U = m * 2*π*(R+r)/2 = π * (R+r) * m
Bei der Berechnung der Mantelfläche eines Rotationskörpers taugt die Verwendung von Zylinderscheiben nicht, denn man würde in der Grenzwertbetrachtung die Höhe h anstatt m einsetzen. h ist aber die Kathede eines rechwinkeligen Dreiecks. Die Hypothenuse m ist auch in der Grenzwertbetrachtung immer länger.
Im Fall des Volumens verhält es sich umgekehrt, denn das Volumen eines Kegelstumpfs ist für identisches h kleiner als das eines Zylinders.
Die Beziehung m² = (R-r)² + h² bleibt auch in der Infinitesimalrechnung erhalten. Anders gesagt gelten die Rechengesetze auch bei unendlich kleinen Zahlen, und somit macht es einen Unterschied, ob man unendlich viele m's oder unendlich viele h's aufaddiert.
Habe ich das richtig verstanden, dass infinitesimal kleine Unterschiede immer gleich 0 gesetzt werden können (z.B. R+r=2R), außer wenn die entsprechende Größe als eine Funktion von dx dargestellt werden kann (z.B. dL = \sqrt{1+{f(x)}^2} dx)? Dann wäre das Volumen mit infinitesimal kleinen Kegelstümpfen auch gleich wie das mit Zylindern, zumindest wenn ich keinen Fehler gemacht habe.
Ich erkläre es mal so: man könnte doch auch die Bogenlänge einer Funktion im Intervall [a,b] über die Summe aller dx-Anteile berechnen, weil sich die dx-Anteile immer mehr dem Funktionsverlauf anpassen. Am Ende ergibt sich aber nur die Differenz b-a.
Bei der Mantelfläche ist der Verlauf der Kurve, die den Mantel beschreibt, entscheidend. Nehme als Beispiel das Intervall [0, 2 Pi] und einmal die Funktion f(x) = 1, das ergibt rotiert um die x-Achse einen Zylinder. Das Integral über f(x) liefert 2 Pi. Zum zweiten betrachten wir die Funktion g(x) = 1 + sin(x). Das Integral über g(x) liefert auch 2 Pi, aber die Mantelfläche durch Rotation um die x-Achse ist eine andere als bei f(x). Anschaulich gesprochen entsteht das dadurch, dass bei g(x) der Mantel "gedehnt" ist, im Bereich [0, Pi] ist er im Vergleich zu f(x) nach innen gedrückt, im Bereich [Pi, 2 Pi] nach aussen gedehnt.
In der Formel zur Berechnung der Oberfläche kommt daher ein Faktor Wurzel( 1 + f'(x)^2 ) bzw. Wurzel( 1 + g'(x)^2 ) vor, der für die genannten Funktionen zu einer unterschiedlichen Mantelfläche führt.
OK, also dass man infinitesimal kleine Kegelstümpfe verwendet, verstehe ich, aber ich verstehe noch nicht so ganz, warum die Mantelfläche des infinitesimal kleinen Kegelstumpfes gleich der infinitesimal kleinen Bogenlänge mal der infinitesimal kleinen Höhe ist. Wenn man so einen aus Papier gebastelten Kegelstumpf nimmt, den senkrecht aufschneidet und dann ausrollt, erhält man ja eine Art "gekrümmtes Trapez". Und wie man davon die Fläche berechnen soll, erschließt sich mir nicht.
Und was ich auch nicht verstehe ist, warum man das beim Volumen mit infinitesimal kleinen Zylindern machen kann, und dafür nicht auch infinitesimal kleine Kegelstümpfe braucht. Ich dachte, dass geht einfach, weil die Zylinder infinitesimal klein sind, und dadurch als unendlich dünne Scheibe gar nicht die Form eines Kegelstumpfes haben können, aber warum ist das bei der Mantelfläche dann nicht auch so?
Das Prinzip mit den infinitesimal kleinen Scheiben ist bei beiden dasselbe und wird bei beiden angewandt.
Die Funktion wird integriert.
Beim Volumen wird das Integral nochmal quadriert. Das bestimmte Integral von A nach B bestimmt und anschließend mit pi multipliziert:

Beim der Mantelfläche entfällt das Quadrieren. Das bestimmte Integral von A nach B wird einfach mit pi multipliziert.
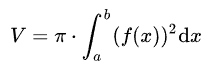
OK, also dass man infinitesimal kleine Kegelstümpfe verwendet, verstehe ich, aber ich verstehe noch nicht so ganz, warum die Mantelfläche des infinitesimal kleinen Kegelstumpfes gleich der infinitesimal kleinen Bogenlänge mal der infinitesimal kleinen Höhe ist. Wenn man so einen aus Papier gebastelten Kegelstumpf nimmt, den senkrecht aufschneidet und dann ausrollt, erhält man ja eine Art "gekrümmtes Trapez". Und wie man davon die Fläche berechnen soll, erschließt sich mir nicht.
Und was ich auch nicht verstehe ist, warum man das beim Volumen mit infinitesimal kleinen Zylindern machen kann, und dafür nicht auch infinitesimal kleine Kegelstümpfe braucht. Ich dachte, dass geht einfach, weil die Zylinder infinitesimal klein sind, und dadurch als unendlich dünne Scheibe gar nicht die Form eines Kegelstumpfes haben können, aber warum ist das bei der Mantelfläche dann nicht auch so?