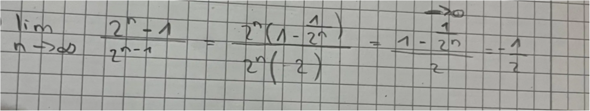Hallo? Ich soll den Grenzwert berechnen die Lösung ist zwei. Ich bekomme immer ein halb raus. Was mache ich falsch?

3 Antworten
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
rechnen, Funktion, e-Funktion
Hallo,
2^(n-1) im Nenner schreibst Du zu (1/2)*2^n um.
1/2 im Nenner kann zu 2 im Zähler umgeschrieben werden.
So bekommst Du 2*(2^n-1)/2^n.
Nun Zähler und Nenner durch 2^n kürzen ergibt 2*(1-1/2^n)/1.
Wenn n gegen unendlich geht, geht 1/2^n gegen 0. Es bleibt als Grenzwert
2*(1/1)=2.
Herzliche Grüße,
Willy
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
rechnen, Funktion, Ableitung
Anderer Weg:
Bruch zerlegen in zwei Teil:
2^n/2^(n-1) = 2^(n-n+1) = 2
und 1/2^(n-1) geht gegen 0.
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
rechnen, Funktion, e-Funktion
die Frage war schon mal von Dir

und hier hast du drei Antworten bekommen

aber du hast nichts gelesen , denn
2^(n-1) ist nun mal nicht 2^n * ( 1 - 2 )
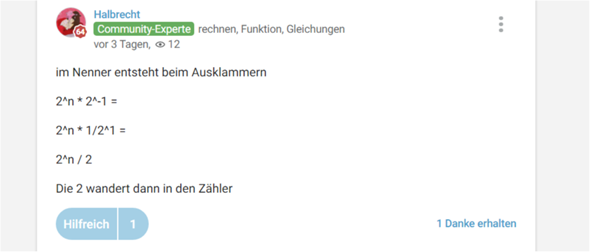
denn 2^(n-1) = 2^n * 2^-1 Potenzregel
und weitere Basics 2 hoch -1 ist 1/2^1