Exponentialfunktion?
.

Darf man nen GTR oder PC dafür nutzen? Sonst müsste man es manuell machen, oder gar ne Linearisierung.
Also mir ging es eher darum wie ich a und q herausfinde
4 Antworten
Vom Prozess her müsste es eine Exponentialfunktion geben. Denn die Glucose nimmt ab, und damit sinkt die Geschwindigkeit weiterer Umwandlung bis zum Gleichgewichtszustand.
Allerdings haben die Daten Ungenauigkeiten und Ausreisser, so dass es keine eindeutige und schöne Kurve gibt.

Als einfache Näherung würde ich mal Tag 5 mit 80 (statt 81) annehmen, dann hast du grad die Halbwertszeit von 4 Tagen ab Tag 1 (160 -> 80).
Am Tag 9 wäre es dann 40 usw.
Nachtrag edit2: Lösung mit dieser Näherung:
Ich hatte zuerst übersehen, dass der Startwert ja 183 ist (t=0), und nicht 160 "am Tag 1".
Die Näherungsmethode bleibt sich gleich, man kann zwei Werte nehmen, die sich möglichst genau halbieren. Also von 160 auf 81, das wäre ungefähr die Hälfte und damit die Halbwertszeit von 4 Tagen.
- Basis 2
- Start bei t=0 mit 183, t=1 ist 160, t=5 ist 81
- Variable x = Zeiteinheit, hier Tage
- Halbwertszeit 4 Tage (Zeiteinheiten)
- Angenommener Endwert (Asymptote): 0% Glucose
- am einfachsten mit Basis 2, was das naheliegendste ist.
- wenn's unbedingt eine e-Funktion sein muss, dann halt mit e und auch ln(2); ergibt die gleiche Kurve (blau)
- oder die rote Kurve mit Halbrechts Näherungsmethode (die mit dem ersten und letzten Wert arbeitet: wie wird in 7 Schritten 61 aus 183?)



ist einfach nur "dumme" Schule . Daher ist eher meine Antwort Standard
wobei die Schüler sich für q auch andere Datenpaare aussuchen können
Suchst du effektiv die Funktion?
Geht es um eine Überschlagsrechnung oder um höchste GEnauigkeit (was bei so einer unexakten Messreihe wenig Sinn ergäbe).
Darfs du elektronische Hilfmittel einsetzen oder geht es um das tiefere Verständnis einer Exponentialfunktion?
Bei solche klar erkennbaren Halbierungs-Vorgängen würde ich als Basis die 2 nehmen (nicht e, sonst musst du auch den ln(2) noch als Faktor einsetzen)
Schulaufgabe , da kann man so vorgehen
183 * x^7 = 61
x = 7teWurz(61/183)
x = 0.85
f(x) = 183 * 0.85^x
mach ne exponentielle Regression, mit m TR oder Excel.

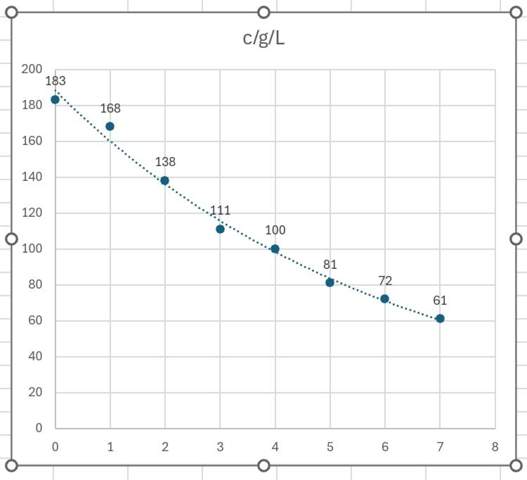
Exponentialfunktion?
Nein, die Daten sehen nicht nach einer Exponentialfunktion aus
Sondern?
Mathematisch passt es zwar nicht exakt, aber als naturwissenschaftliche Ausgleichslinie schon, wenn auch mit Abweichungen.